初版

CPLDでLチカ [Xilinx XC95144XL]

電子工作ということで、モジュールの組み合わせではなく、実際の回路設計っぽいことを書いて見ました。 PLDが使えるようになると、CPUと組み合わせて色々できることが広がると思います。 # 使用した物 - Xilinx CPLD XC95144XL-10TQG144 - クリスタルオシレーター 50MHz KDK HHC50ATW - LED - 抵抗 330Ω - 電解コンデンサ 16V 47μF - 変換基板 DAISEN Q144 - ピンヘッダ(L型2列) ※完成済みのボードではなく、すべての回路を自分で作成です。 以下、キーとなる部品について記載します  ### CPLD タイトルにもなっている今回のキモです。 大分類としてPLDと分類される部品で、チップ内の回路を自由に書き換え可能なICです。 PLDカテゴリの他の部品では、GAL、FPGA等があります。 書き込み可能な回路の大きさは、GAL<CPLD<FPGAとなります。 CPUではありませんので、プログラムを実行するものではありません。 FPGAくらいの規模になると、自分でCPUを設計することも可能です。 今回は使用したのはXilinx社製のXC9500XLシリーズ「XC95144XL-10TQG144」というCPLDで、 &nbsp; 　XC95:XC9500シリーズ &nbsp;　144マクロセル(レジスタ数≒メモリ容量) &nbsp;　XL:XLシリーズ＝3.3V動作 &nbsp;　-10:10ns≒約100MHzまで動作 &nbsp;　TQ:TQFPパッケージ(ギリギリ手ハンダできるレベル) &nbsp;　G:鉛フリー &nbsp; 　144:144pin(≒I/Oポート数) というスペックの物です。 ### クリスタルオシレーター 基準となるクロックです。今回は50MHzを使用しました。 データシートでは5V用となっていますが、パーツ屋さんが3.3Vでも動くよと教えてくれたのでこちらを使っています。 正式に3.3V対応品でピンが付いていてブレッドボードなどで使える物は入手が難しいです。 ### 電解コンデンサ 電圧変動対策として電解コンデンサを入れています。 このCPLDは構造的にフラッシュメモリなので、回路の書き込み時にわりと電力を消費し、動作が不安定になることがあります。その対策のためにコンデンサを接続します。 耐圧は3.3Vを十分に上回るものであれば6.3Vなどでも問題ありません。容量は本来は変動量などを測定して設定すべきですが、個人的な実験であればカット＆トライの選定で適当でいいでしょう。 ちなみに使う個数は1個ですが、写真では実装済みと未使用の２つが写ってます。 # Lチカ回路を作成する(物理) 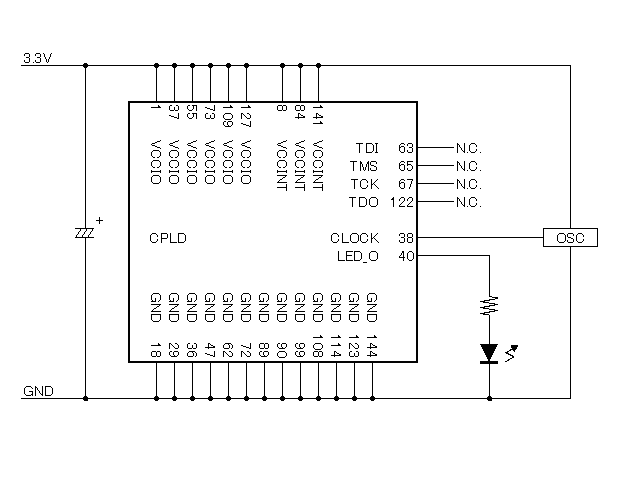 さて、ここはまずブレッドボードや変換基板上に作成している回路です。 といっても、検討する事はLEDの抵抗値くらいで、Arduino等のLチカと考え方は全く同じですので省略します。 あとは電源などの接続だけです。 このCPLDの電源にはVCCIOとVCCINTという2系統の電源が必要です。 VCCIOはIOの動作電圧(「1」を出力のときに出力される電圧)を決定するための電源で、VCCINTは内部動作の為の電源です。 XC9500XLシリーズではどちらも3.3Vで動作されることが可能ですので、結果としてはどちらも同じ電源を接続することになります。 TDI/TMS/TCK/TDOは未接続(N.C.)ですが、作成した回路データをチップに書き込む際に使用します。 # Lチカ回路を作成する(ソース) 回路の作成といっても、HDLといわれる回路記述用の言語を使用して記載します。 Verilog-HDL、もしくはVHDLというどちらかの言語を使用する場合がほとんどです。 今回はVerilog-HDLを使用します。 ```html:top.v module top(CLOCK, LED_O); input CLOCK; output LED_O; reg [25:0] count; always @(posedge CLOCK) begin count <= count+1; end assign LED_O=count[25]; endmodule ``` reg宣言部で、countという26bitのレジスタ(アセンブラでいうところのレジスタに相当)を定義しています。 次に、always文で動作タイミングを定義しています。 この例では、CLOCKがposedge(0→1へ変化したとき)に、begin～endの中身が処理されます。 ですので、1クロックごとにcountがインクリメントしていきます。 足し算回路自体は自分で設計しなくても、ツールがいい感じに自動生成してくれます。便利ですね。 最後に、assign文で、countの最上位bitをLED制御端子に接続しています。 26bitなので、67108864カウントで1周します。クロックが50MHzなので、約1.3秒周期で点滅することになります。 そして、もう一つ必要なファイルがあります。 ```html:top.ucf NET "CLOCK" LOC = "P38" ; NET "CLOCK" PERIOD = 20.0ns HIGH 50% ; NET "LED_O" LOC = "P40" ; ``` ソースファイルの信号が、実際に物理的にチップのどこの端子に接続されるかという設定ファイルです。 P38(38pin)がCLOCK、P40(40pin)がLED_Oと定義しています。 # Lチカした!  XC9500シリーズは結構古いデバイスなので、最新のXilinxの開発キット(vivado)では対応していません。 EOL品では無いんですけどね・・・。 ですので、ISEを使用して書き込むことになります。 ツールの使用方法はここのページのメインではなさそうな気がしますので、ISEの使用方法は省略しますが、TDI/TMS/TCK/TDOを専用のダウンロードケーブルに接続して書き込みを行います。 # 実際にどんな回路が書き込まれたの？ さて、あくまでPLDは回路を書き込むのであり、プログラムを書き込むものではありません。 やや語弊はありますが、上記ソースを回路図にしたものが書き込まれます。 回路図はツールがソースから自動で作成してくれるのですが、どのような回路が作成されたかを予想してみましょう。 まず、回路要素として必要な物は、regで定義された26ビットのレジスタ。 これは、D-FF(フリップフロップ)というもので構成されます。 D-FF1つで1bitの情報を保持できるので、26個のD-FFが使用されます。 XC95144では144マクロセルなので、最大144個のD-FFを使用する回路が作成できます。ですので、まだまだ余裕はありますね。 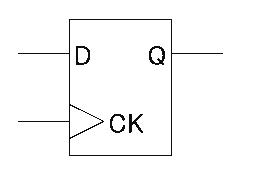 動作は非常に簡単で、CLOCK入力が0→1に変化したときのDに入力されている値を保持し、Qに出力しつづけます。それだけです。 次に、必要になるのは足し算回路です。count+1の部分ですね。 まず、2進数の足し算はどのように行われるかを考えましょう。 考え方は10進数と同様です。 ここでは、「11」+「01」を例にします。 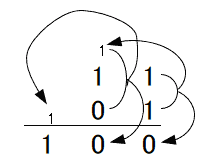 まず、最下位bitの「１」と「１」を加算します。結果は「１０」となり、繰り上がりが発生します。 次に、一つ隣の上位bitの計算をします。ここでは、「１」と「０」と「繰り上がってきた１」の加算します。 結果は「１０」となり、ここでも繰り上がりが発生します。 結果、「１１」＋「０１」＝「１００」となります。 このような計算方法を実現するためには、まず、任意の一桁の答えを計算するために必要な要素を考えます。 任意の一桁を計算するためには - 足す数(A) - 足される数(B) - 下位桁からの繰り上がり値(Carry IN=CI) の３入力が必要で、計算結果としては、 - 足した結果(Sum=S) - 繰り上がり(Carry OUT=CO) の２出力となります。これらを表にまとめて、取り得る値を全て考慮すると、８通りのパターンがあり、 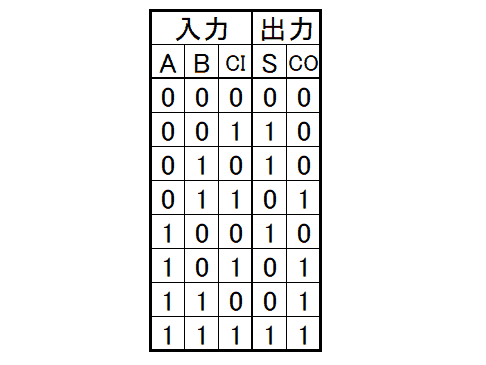 となります。これは、任意の桁数の足し算回路を実現するために必要となる、1bit分の加算論理となります。 これを、全加算器(Full adder)と言います。 さて、この表を実際に回路として設計するためには、カルノー図やクワインマクラスキー法とかがありますが詳しくは省略し、結果だけを書きます。 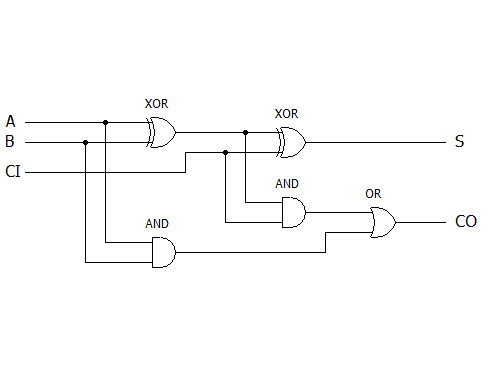 MIL記号といわれるANDやORが出てきました。 これらの部品を組み合わせることで、先ほどの表と同じ結果を得られる回路になっています。 ※実際にはAND等それ自体がmosという部品を組み合わせた回路なのですが、表からかけ離れていくので触れないことにします。 さて、これで1bit分の加算回路ができました。 これを多bit化するためには、この全加算器を数珠つなぎにしていくだけでできます。  はい、これで4bit+4bitの加算機ができました。さらにbitを増やす場合も同じですね。 では最後にこれをD-FFに接続しましょう。 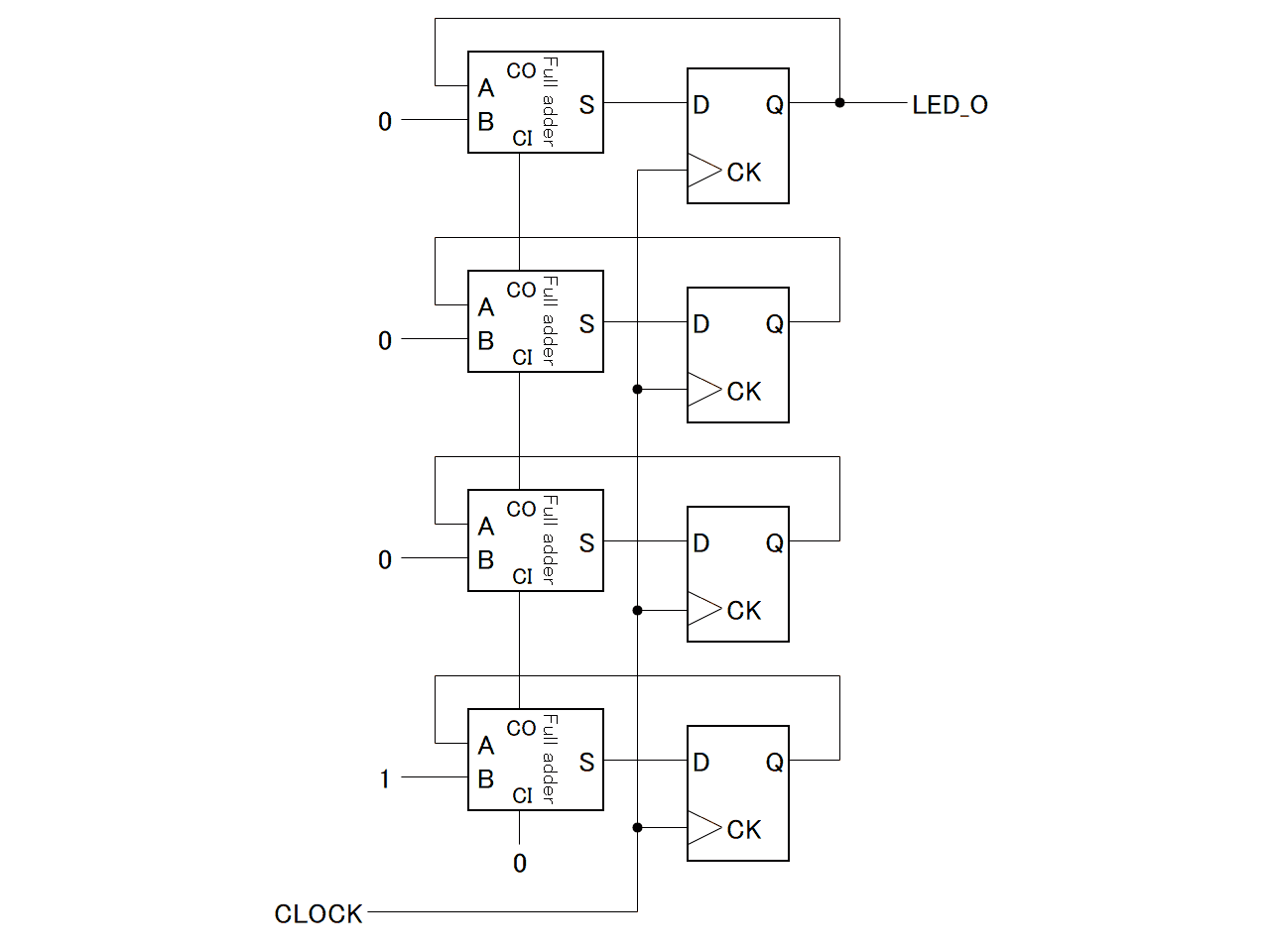 書き方の都合で加算器が90度回転していますが、これが今回作った回路(を4bitに減らした物)です。 実際には、カウンタが常に「＋１」なので、全加算器の片側の入力は0か1に固定されるので、さらに全加算器の回路を各bit毎に簡略化することは可能ですね。 # 最後に 実は、PLDってどういう仕組みで回路が書き込めるのかということを調べると、実際のところはこのような回路が構成される訳では無く、全然別な仕組みで動いているのですが、回路を設計する、ということで、このような解説としました。 PLDを使うメリットは、速度が出せるというのが最大のメリットではないでしょうか。 この記事では50MHzを約7000万分周していますが、2分周で正確に25MHzでLEDを点滅なども容易に可能です。このくらいの速度になると、ArduinoなどのCPUで制御では難しいでしょう。 # 参考文献 XILINX XC95144XL High Performance CPLD (DS056) 　英語版(v2.0)　https://japan.xilinx.com/support/documentation/data_sheets/ds056.pdf 　日本語版(v1.4)　https://japan.xilinx.com/support/documentation/data_sheets/j_ds056.pdf XILINX XC9500XL High-Performance CPLD Family Data Sheet (DS054) 　英語版(v2.5)　https://japan.xilinx.com/support/documentation/data_sheets/ds054.pdf 　日本語版(v2.2)　https://japan.xilinx.com/support/documentation/data_sheets/j_ds054.pdf KDK Crystal Oscillators 　http://www.kdk-group.co.jp/04pdf/clock-22-hht&hhc.pdf