初版

エミッタ接地回路の入力抵抗

覚え書き兼 Elchika の数式モードの練習のために書きました。 バイポーラトランジスターは、FETとは異なり、入力抵抗がほぼ無限大とみなすことはできません。具体的にはどう計算するのでしょうか。 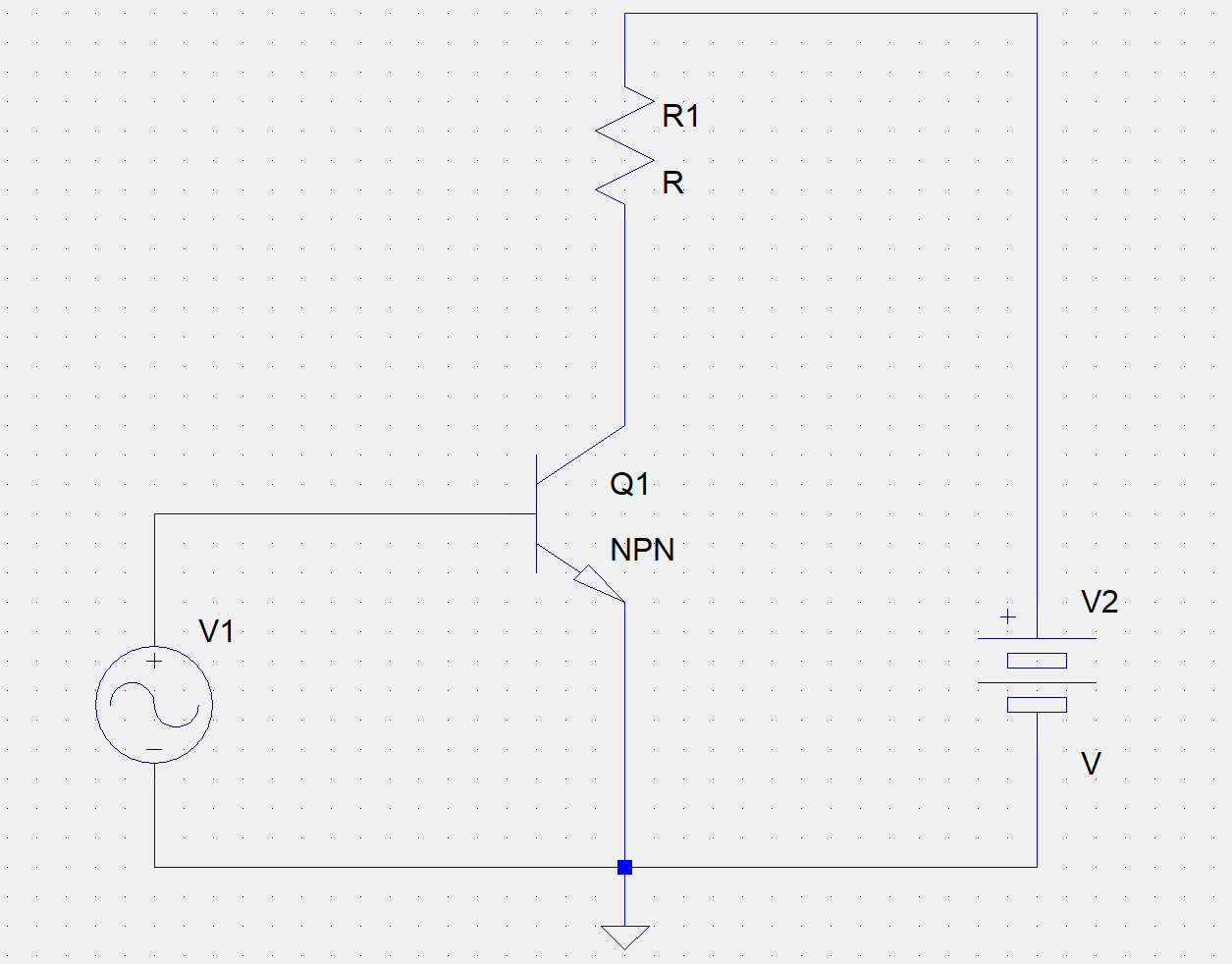 今、適切なバイアスがされて、 $$I_\text{C} = h_\text{FE} I_\text{B}$$ の電流が流れているとします。 このとき微小信号に対する入力抵抗は、 $$r_\text{in} = \frac{h_\text{FE} V_t}{I_\text{C}} = \frac{V_t}{I_\text{B}}$$ で求められます。 ここで、*IBを基準に見れば、トランジスター個別の特性 (hFE) が全く出てこない*ところが興味深いところです。 入力抵抗が大きいと、いわゆる「ロー出しハイ受け」がしやすくなり、回路の自由度が上がります。しかしそのためにはベース電流を小さくする必要があり、増幅率は下がり、高周波特性や雑音特性も悪くなります。このトレードオフはどの品種を選ぼうと、バイポーラトランジスターである限り逃れられません。 Vtは熱電圧といい、温度で決まる定数です。常温の時のVtは約26[mV]となります。 $$V_t = \frac{kT}{q}$$ kはボルツマン定数[J/K]、Tは絶対温度 [K]、qは電子の電荷[C]です。 ここで、ベース電流の単位をμA、熱電圧の単位をmVにすると、入力抵抗の結果の単位がkΩと扱いやすい値になり、計算が簡単になります。 実際に例を上げてみると IB = 1[μA] のとき、rin = 26 / 1 = 26 [kΩ] rin = 100 [kΩ] となるベース電流は、IB = 26 / 100 = 0.26 [μA] となります。