初版

ステッピングモーターのインピーダンスと消費電力を測ってみた

セットアップや使用方法

ユニポーラステッピングモーター [SPG27-1101](https://akizukidenshi.com/catalog/g/gP-11839/) のコイルのインピーダンスおよび消費電力を計測してみました。写真は自作の制御基板に接続した SPG27-1101 です。  SPG27-1101 のデータシート[^1]によると、ピン配置は次の通りです。  Φ1C や Φ2C はセンタータップと呼ばれる端子です。この端子はバイポーラ型のモーターにはない、ユニポーラ型に独特の端子です。バイポーラ型とユニポーラ型のコイルの巻き方は [ステッピングモータの駆動：バイポーラ結線とユニポーラ結線 ｜ TechWeb motor](https://techweb.rohm.co.jp/motor/knowledge/basics/basics-04/496) が詳しいです。 ## インピーダンスの計測 ユニポーラステッピングモーターは、センタータップに電源のプラス端子をつなぎ、コイル両端にトランジスタを接続して電流を引っ張る形で駆動します。そのため、今回のインピーダンス計測はコイル端（Φ1）とセンタータップ（Φ1C）の間に対して行いました。他のコイル端やセンタータップでもほぼ同じ特性になることが期待されます。  グラフには Z、Rs、Xs を表示しています。実線が Z、破線が Rs、点線が Xs です。Rs や Xs の添え字 s は「直列接続」を表す英語「series」の頭文字です。抵抗器と純粋なコイルが直列に接続された等価回路における抵抗値とリアクタンスであることを意味しています。 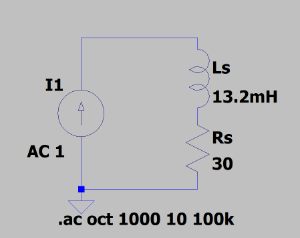 グラフ左端（10Hz）では Rs=30Ω、Xs=1Ω 程度になっています。周波数に比例して Xs が増加していくことが分かります。データシートによるとコイル抵抗は 30Ω ですので、周波数が低い領域における Rs の測定結果はデータシート通りです。 20kHz くらいまでは誘導性（コイル）負荷、それより高い周波数では容量性（コンデンサ）負荷となっていることが分かります。Rs は 200Hz 付近までは周波数に依存せず一定値ですが、その先は徐々に上昇しています。測定対象が等価回路通りならば Rs は常に一定だと思うのですが、モーターのコイルは等価回路通りではないということかと思います。 データシートによると大体数百 Hz 程度の PWM 信号で駆動することを想定しているようです。グラフの 500Hz のところを読むと、インピーダンス（Z）は 56.41 Ω、リアクタンス（Xs）は 41.54Ω と表示されています。 ## 消費電力の計測 データシートには SPG27-1101 の入力定格は「平均消費電力 5W 以内」とあります。500Hz の PWM で駆動した場合の消費電力を計測してみたいと思います。ただ、消費電力を直接計るのは難しいので、電流を計ってから消費電力を計算することにします。電流計測回路は次の通りです。 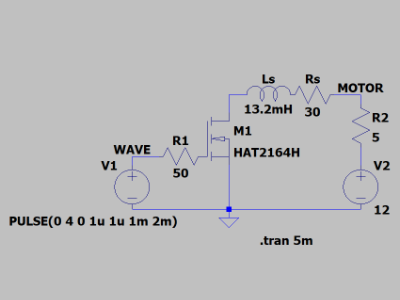 M1 を 500Hz の矩形波でスイッチングさせたときの電流の変化を計る回路です。Ls と Rs がモーターコイルの等価回路です。インピーダンスの計測結果より、直列に 30Ω の抵抗があるとしてモデル化しました。Ls の値（13.2mH）は 500Hz の地点におけるリアクタンス Xs の値から計算しました[^2]。 電流を計るために、電流検出用の抵抗 R2 を直列に挿入し、その両端電圧から電流を計算します。電流検出用の抵抗は一般的にはもっと抵抗値の低いものを使いますが、手元に無かったので 10Ω の金属被膜抵抗 2 本を並列にして電流検出抵抗としました。 交流回路において、エネルギーを消費するのは抵抗だけで、コイルやコンデンサのリアクタンス成分はエネルギーを消費しません。従って、モーターを流れる電流が分かれば消費電力は $I^2R_S$ で計算できます。  シミュレーション結果を示します。緑のグラフが V(wave)、つまり WAVE 点の電圧です。見ての通り、0V と 4V を繰り返す矩形波です。青のグラフが V(motor) で、MOTOR 点の電圧を示します。後で示す実測結果に表示されているのはここの値です。赤のグラフが I(Rs) で、抵抗 Rs に流れる電流を示します。V(motor) を計測することによって I(Rs) を計算しよう、というのがこの後の実測でやりたいことです。  これはモーターの Φ1 - Φ1C 間について V(motor) を計測した結果です。シミュレーションとほとんど同じ形になっていますね。縦軸 1 目盛りが 2V ですので、スイッチオンの瞬間から電圧が下がり始め、最大 1.7V 程度の電圧降下が発生していることが分かります。ということは、その瞬間には 1.7V/5Ω = 0.34A の電流が流れている計算になります。 ## 消費電力の計算 平均の消費電力に興味があります。まず瞬時電力を求め、それを積分することで求めます。そのために、まずは各時刻における電流値を求めてみましょう。R2 による電圧降下を数式で近似すると、大体次のようなグラフになります。縦軸が電圧（V）、横軸が時刻（ms）です。 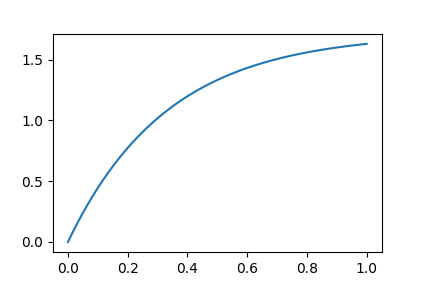 このグラフの数式は $\frac{12R_2}{R_S+R_2}(1-e^{-3t})$ です。係数 $\frac{12R_2}{R_S+R_2}$ はモーターに直流を流した場合に R2 にかかる電圧です。これが指数関数の漸近線になります。 時刻 t の係数 -3 はグラフの形が計測結果に一致するような値を選びました。計算で求めたのではなく、目測です。 500Hz の PWM 周期のうち 1ms 間は電流 0、その後 1ms で指数的に電流が増えます。各時刻における電流は次の表のようになります。 | 時刻 t (ms) | R2の両端電圧 (V) | 電流 I (mA) | |---------------|------------------------|--------------| | -1～0 | 0 | 0 | | 0～1 | $\frac{12R_2}{R_S+R_2}(1-e^{-3t})$ | $\frac{12}{R_S+R_2}(1-e^{-3t})$ | 瞬時電力は $I^2R_S$ ですので、平均電力 $P$ は次の通りです。 $$ P=\frac{1}{1-(-1)}\int_{-1}^{1}I^2R_Sdt\approx 0.94 $$ この平均消費電力はコイル 1 つ分です。SPG27-1101 は 2 相励磁で制御しますので、同時に 2 つのコイルが駆動されます。従って、500Hz の PWM で駆動した場合の平均消費電力は 0.94×2=1.88 (W) となります。 [^1]: ステップ角度 15 °で小型ステッピングモータ SPG27-1000 シリーズ, 日本電産コパル電子, https://www.nidec-copal-electronics.com/j/catalog/stepping-motor/spg27-1000.pdf [^2]: $X_S=2\pi fL$ より $L=\frac{X_S}{2\pi f}=\frac{41.54}{2\pi\times 500}\approx 13.22$