初版

正弦波全波整流回路の平滑コンデンサ容量計算式

セットアップや使用方法

抵抗負荷Roにおける平滑コンデンサC = 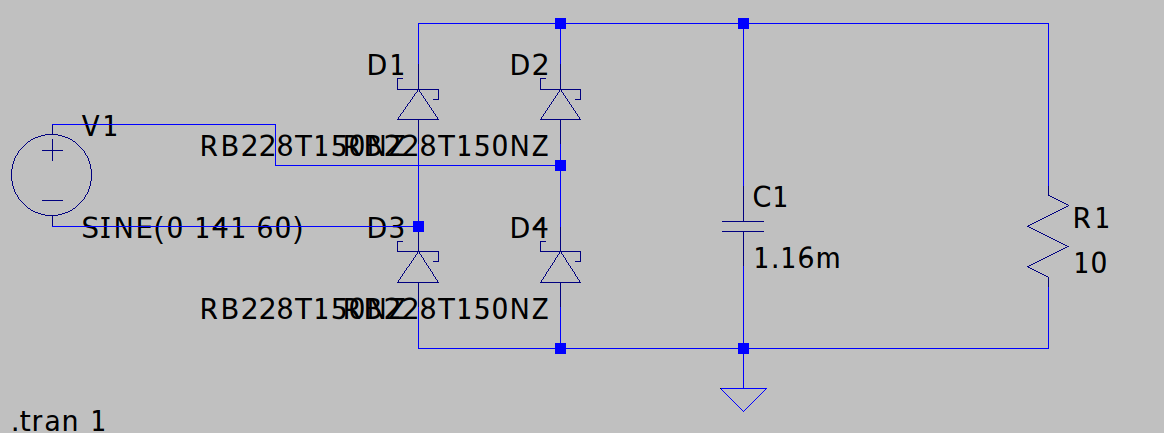 $${C=-\frac{\frac{\pi}{2}+sin^{-1}(\frac{Vout_{min}}{V_{out_{max}}})}{2{\pi}fR_o{\times}ln(\frac{V_{out_{min}}}{V_{out_{max}}})}}$$ ただし $${\frac{V_{out_{min}}}{V_{out_{max}}}=\eta}$$ とすると $${C=-\frac{\frac{\pi}{2}+sin^{-1}(\eta)}{2{\pi}fR_o{\times}ln(\eta)}}$$ 半波整流回路は、全波整流より波の間隔がさらにπ空くので $${C=-\frac{\pi+\frac{\pi}{2}+sin^{-1}(\eta)}{2{\pi}fR_o{\times}ln(\eta)}=-\frac{\frac{3\pi}{2}+sin^{-1}(\eta)}{2{\pi}fR_o{\times}ln(\eta)}}$$ 合ってるかは分からないけど... 導出 = まずRC並列回路の放電時の電圧は、初期の最大電圧をVmとして $${V_C=V_{m}e^{-\frac{t}{RC}}}$$ よりtは $${t=-RC{\times}ln(\frac{V_C}{V_m})}$$ ただし、全波整流回路の放電が開始される際の角度はπ/2なので $${t-\frac{\pi}{2\omega}=-RC{\times}ln(\frac{V_C}{V_m})\space\space\cdot\cdot\cdot A}$$ また、正弦波交流の電圧瞬時式は $${V=V_m{\times}sin(\omega t)}$$ コンデンサが再充電される際は、角度がπ以上であるため $${V_C=V_m{\times}sin(\omega t - \pi)}$$ より再充電が開始される時間tは $${t=\frac{1}{\omega}(sin^{-1}(\frac{V_C}{V_m})+\pi) \cdot\cdot\cdot B}$$ B式をA式へ代入し $${\frac{\pi}{2}+sin^{-1}(\frac{V_C}{V_m})=-\omega RC \times ln(\frac{V_C}{V_m})}$$ Cの式へ整理しVC=Voutmin,Vm=Voutmaxに変換してやると $${C=-\frac{\frac{\pi}{2}+sin^{-1}(\frac{Vout_{min}}{V_{out_{max}}})}{2{\pi}fR_o{\times}ln(\frac{V_{out_{min}}}{V_{out_{max}}})}}$$ θ同士の比が静電容量になるという面白い式になりました。 定電流負荷の場合 = 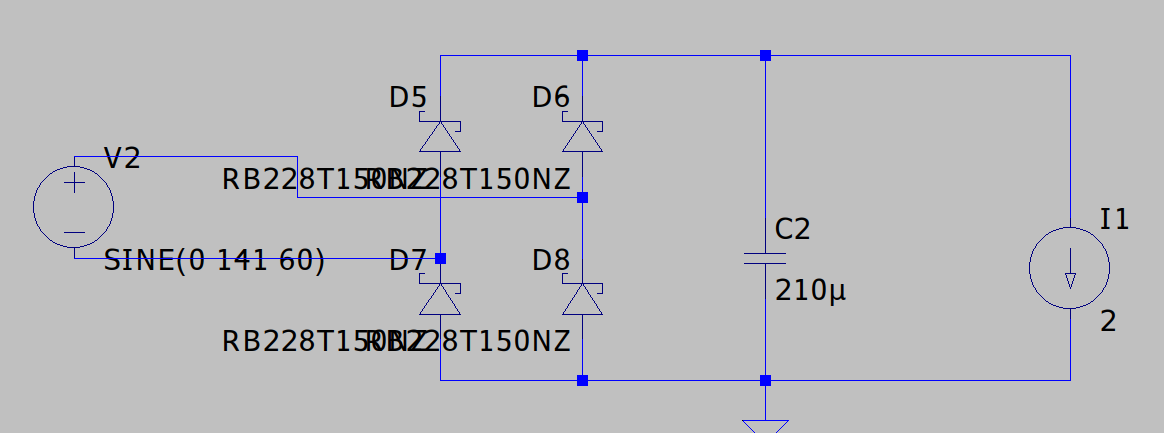 $${V_C=\frac{1}{C}\int idt}$$ よりiはコンデンサ自身から発生しているので負になります。つまり $${V_C=-\frac{i}{C}t+K}$$ 放電開始時t=π/(2ω)とおき、そのときVCはVmなので $${K=V_m+\frac{\pi i}{2\omega C}}$$ より $${V_C=V_m-\frac{i}{C}(t-\frac{\pi}{2\omega})}$$ より $${t-\frac{\pi}{2\omega}=\frac{C(V_m-V_C)}{i}}$$ この式に前述のB式を代入し $${\frac{\pi}{2}+sin^{-1}(\frac{V_C}{V_m})=\frac{\omega C(V_m-V_C)}{i}}$$ Cの式へ整理しVC=Voutmin,Vm=Voutmax,i=Ioutに変換してやると $${C=\frac{\frac{\pi}{2}+sin^{-1}(\frac{V_{out_{min}}}{V_{out_{max}}})}{2\pi f(V_{out_{max}}-V_{out_{min}})}I_{out}}$$ 半波整流回路の場合は $${C=\frac{\frac{3\pi}{2}+sin^{-1}(\frac{V_{out_{min}}}{V_{out_{max}}})}{2\pi f(V_{out_{max}}-V_{out_{min}})}I_{out}}$$