初版

PFM発振器をLTSpiceで作ってみた

製作品

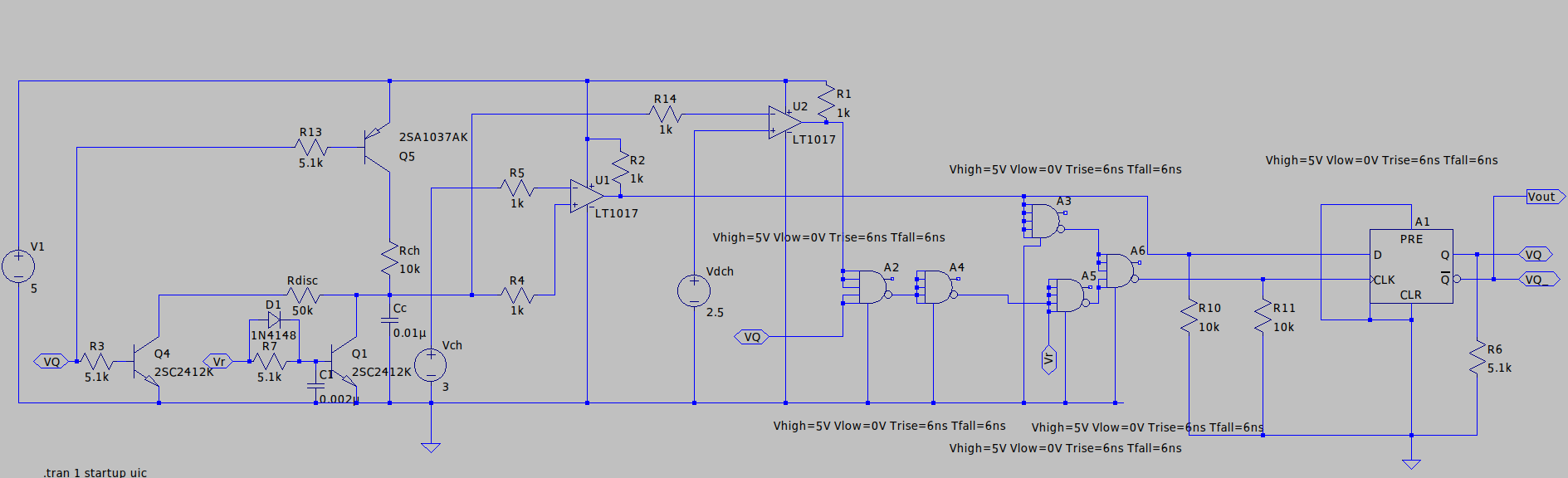
今回はPFM発振回路を考案してLTSpiceで作ってシミュレーションしてみました。 PWM発振回路は沢山あるのですが、オン時間やオフ時間が固定されたPFM発振回路はあまり聞きません。ですので作ってみることにしました。 PFMってなんですの？ = まず、PWM変調はご存知かと思います。この回路は入力のアナログ信号電圧をパルス信号の幅で表現する手法となります。  このときパルスの幅(デューティ比)に対して、パルスの周期が変化しないのが特徴となっています。 一方パルス幅のうち、オン時間もしくはオフ時間を固定すると、パルス幅の変化に伴いパルスの周期(周波数)も変化します。 一方PFMでは、  PWM波形と違い、概ねオン時間が固定されているのがわかります。 波形の通り、デューティ比の高さに比例してパルス周波数が上昇しているのがわかります。 回路 =  まず原理から  (緑の線がコンデンサ波形です。) 1:tonの期間でRchからCcが充電されます。充電電圧は0~Vchまでで、デューティ比に依存しません。またCcの電圧がVchになるとU1の出力が1になり、フリップフロップA1を反転させます。このとき出力が1→0になります。また同時にQ5をoffに、Q4をonにしてCc放電モード(toff)に移行します。 電源電圧をVとすると $${V_{ch}=V(1-e^{-\frac{t_{on}}{R_{ch}C_c}})}$$ つまりtonは $${t_{on}=-R_{ch}C_c\times ln(1-\frac{V_{ch}}{V})}$$ です。 2:Q5がoff,Q4がonになり、toffの期間に入ります。Rdiscを界してCcの放電が開始されます。Ccの電圧がVdchになるとQ6がオンになってCcが完全に放電されます。このとき、フリップフロップA1にU2からパルスが送られて出力を反転し、出力を0→1に反転します。同時にQ6がonになってCcが完全放電されます。またQ5がon,Q4がoffになり、再びtonの期間に入ります。 $${V_{dch}=V_me^{-\frac{t_{off}}{R_{disc}C_c}}}$$ つまりtoffは $${t_{off}=-R_{disc}C_c\times ln(\frac{V_{dch}}{V_m})}$$ このVdchの可変することででtoff期間をさせてデューティ比を変化させます。 このとき $${V_{dch}\leqq V_{ch}}$$ がデューティ比Dを変化できる条件となります。 デューティ比Dは $${D=\frac{t_{on}}{t_{on}+t_{off}}=\frac{1}{1+\frac{t_{off}}{t_{on}}}}$$ より $${D=\frac{1}{1+(\frac{R_{disc}}{R_{ch}}\times \frac{ln(\frac{V_{dch}}{V_m})}{ln(1-\frac{V_{ch}}{V})})}}$$ また、Dが0.5のときton=toffなので、Vdchは $${V_{dch_{0.5}}=V_me^{\frac{R_{ch}}{R_{disc}}\times ln(1-\frac{V_{ch}}{V})}}$$ となります。 Vdch=Vchのときデューティ比Dが1に近づきます。 ちなみに電源電圧V=5V,Vch=3V,Vdch=2.5VとしてCc=0.01uF,Rch=10kΩ,Rdich=50kΩとすると $${t_{on}=-10\times 10^{3}\times 0.01\times 10^{-6} \times ln(1-\frac{3}{5})=91.6[\mu s]}$$ さらにデューティ比は $${D=\frac{1}{1+(\frac{50}{10}\times \frac{ln(\frac{2.5}{3})}{ln(1-\frac{3}{5})})}=0.501}$$ 大体半分になりました。  んーーー、、、トランジスタの素子の応答速度の遅さやその他の容量成分などの原因か、、、tonが10%以上ずれてる気がします。。。。ですけどデューティ比は綺麗かも。。。 んで実験してて思いましたが、コンパレータは入力バイアス電流がnAクラス以下のものでないと正しく動作しない現象に遭遇しています。 ロジック版 - 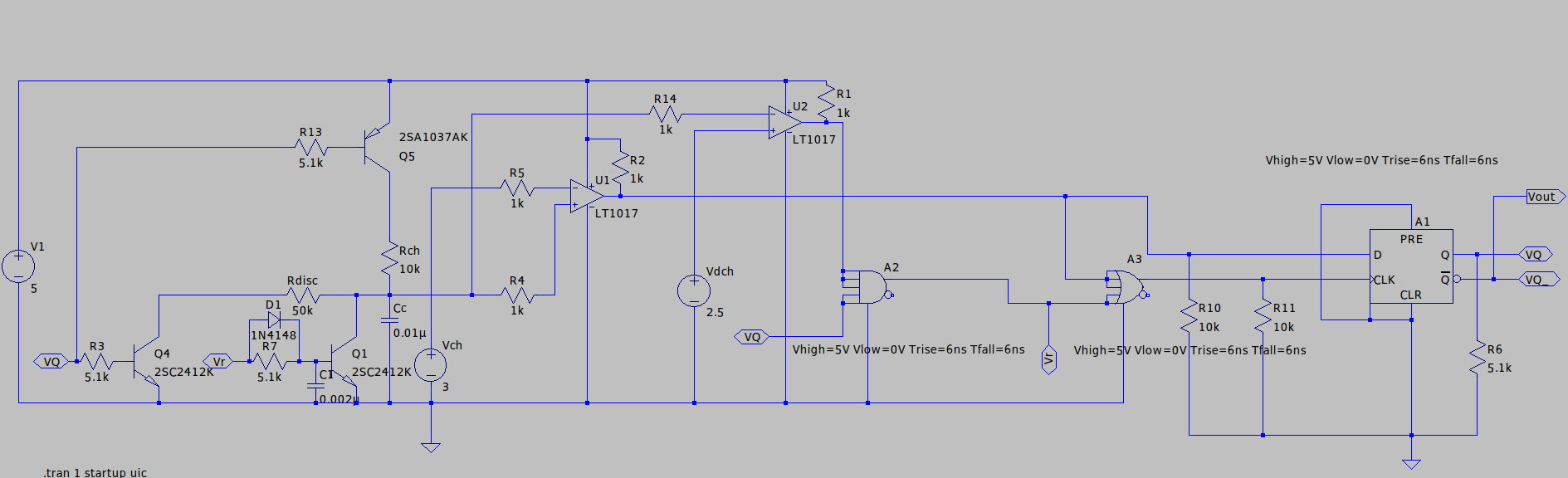 今度はトランジスタとダイオードで再現していた一部部分をロジック化してみました。こうしたほうがいいかもしれません。 動作が早くなりすぎてCcの放電が追いつかなかったので、Q1にC1,R7,D1でデッドタイムを挿入してみました。 ORとANDをNANDで置き換え - ORとAND回路を一々入手するのも面倒だと思います。ですので、ANDとORをNAND回路で作ってみました。 NANDの全入力をショートさせるとOR回路になります。  つまり、ANDはAND*ORになります。 $${\text{AND} =\overline{\text{NAND}}=\overline{\overline{A\cdot B}}}$$  次にOR回路を作ります。 NAND回路はド・モルガンの法則によりNOT入力OR回路に等価できます。 $${\overline{A\cdot B}=\overline{A}+\overline{B}}$$ つまりNAND回路の入力にNOT回路をつけるとOR回路になります。 $${\overline{\text{NOT}_A\cdot \text{NOT}_B}=\overline{\overline{A}\cdot \overline{B}}=\overline{\overline{A}}+\overline{\overline{B}}=A+B}$$  そうしてできたのが以下の回路になります。