フライバックコンバータをLTSpiceで設計してシミュレートしてみた

前回フライバックトランスの計算式を投稿したのですが、今回はLTSpiceで実際にフライバックコンバータを組んでシミュレートしてみたので記事にしておきます。

おそらくブラウン管テレビから高圧トランスを取り出した人なら「フライバックトランス」というのを聞いたことがあると思いますが、その原理を使用した電源になります。
一般的にトランスというのは、巻数比だけで二次電圧を変化させるものとなります。一方でフライバックトランスというのは、巻数比に加えて一次電圧のデューティ比によって二次電圧が変化するものとなります。これを用いたコンバータがフライバックコンバータとなります。またこのトランスを使うことによって、フォワードコンバータの出力側にあるようなフィルタ用コイルを省いたり出力側回路の部品を削減して小さくできます。

https://edn.itmedia.co.jp/edn/articles/1206/11/news010.html

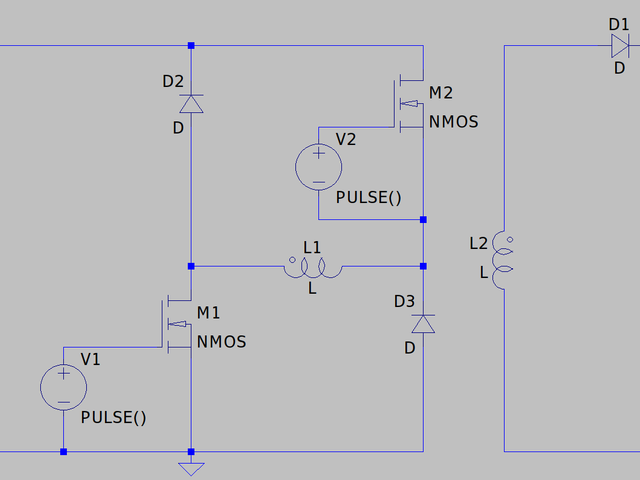
フライバックコンバータは一次側と二次側の巻線の方向が逆向きになっています。またその後ろにダイオードが付いています。
つまり、一次側に電圧が印加されたタイミングで二次側に出力部には電圧が発生せず、電流が流れません。つまりこのときトランスのコアに磁気エネルギーが蓄えられていることがわかります。
一次側がオフすると二次側起電力の極性が逆転して出力に電流が流れ始めます。このときトランスコアの磁気エネルギーが放出されて電流が流れます。
一次電流が流れる時間が二次電流が流れる時間より長いほど、蓄えられたエネルギーを一気に放出しなければならなく出力電圧が上がっていきます。つまり一次電圧のデューティ比に比例して出力電圧が大きくなります。（非絶縁のブーストコンバータやバックブーストコンバータも同じ原理で電圧が変化します。）

(I(L1)が一次電流,I(D3)が二次電流、共振しちゃった...)

今回使うコンバータ用ICがTL494となります。このICは内部にpwm用の発振回路とコンパレータが内蔵され、さらにはオペアンプや基準電圧を搭載していて好みの電源を作ることができます。

https://www.ti.com/jp/lit/gpn/tl494

これだけ見てもまだ分かりにくいかもしれません、、、PWMComparatorに繋がる3番ピンの電圧が0の場合はPWMのデューティ比はほぼ100%に近くなります。またこの電圧の増加に反比例してデューティ比が減少していき、4Vでほぼ0になります。そしてこの電圧をError Amplifierで制御することができます。

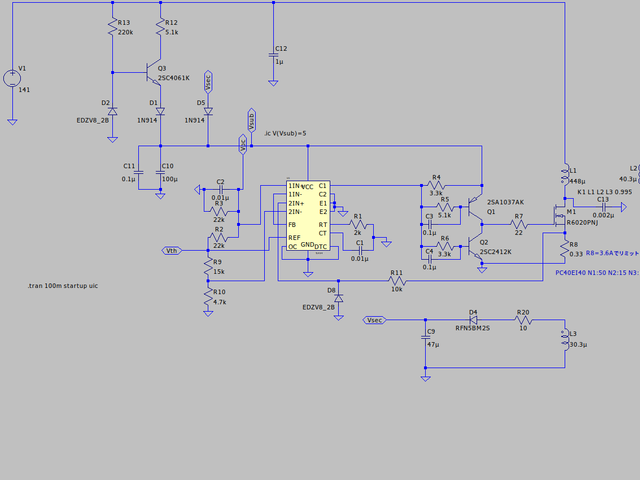
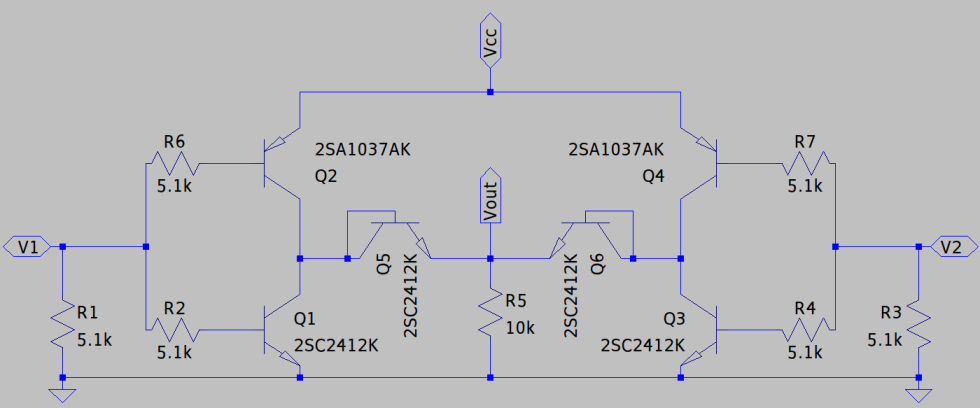
PWMのデューティ比を滑らかに変化させるためにこのような回路にしました。

エラーアンプ1をゲイン1倍で動作させ、1番ピンIN+と3番ピンの電圧を同じにします。R2とR3で基準電圧5Vの半分の2.5Vをつくりデューティ比が大きなPWM信号を作ります。
コンバータの出力電圧が決まった値を上回ったとき、フィードバックされてくる信号によりここの電圧が上がりデューティ比が下がります。フィードバック信号がデジタル的なパルス信号なのでそれを平均化して直流に近づけて制御がなめらかになるようにC2を取り付けています。

TL494のPWM周波数は6番ピンRTと5番ピンCTで決まります。この周波数は

${f_{osc}=\frac{1}{R_1C_1}}$

今回は50kHzとしました。

こちらは出力側に設けられた出力電圧を検出するエラーアンプです。
R14とR15で出力電圧を設定することができます。TL431の基準電圧が2.5Vであり非反転増幅回路の式を用いて出力電圧は

${V_{out}=2.5{\times}(1+\frac{R_{14}}{R_{15}})}$

となります。今回は出力電圧Voutは15VなのでR14=10kΩ,R15=2kΩにしました。
またR18とC8ですが、これが無いと変化の大きなパルス信号がTL494に伝わってPWMのデューティ比が激しく変化し、出力電圧が不安定だったり大きなノイズが発生します。そのためTL494にフィードバックするフォトカプラの応答を遅くするために設置しています。そして前述のC2でさらに変化を遅くして滑らかな制御ができるようにします。シミュレーションで確かめながら値を探ってみてください。

フォトカプラ電流(緑)がパルス状なのに対して、フィードバックされたTL494の1番品電圧(青)が平均化されて直流になっているのがわかります。
続いてR17ですが、TL431に電流が流れ始めるときに制御が不安定にならないようにするための抵抗です。

https://www.ti.com/lit/ds/symlink/tl431.pdf

TL431が完全にオンする領域(Iminと書かれた部分以降)までの間に、非線形に電流が流れ始めて400μAまで増加する領域が存在します。この非線形領域でLEDがオンしないようにしています。つまりR17に400μA以上流せば良いです。余裕をもって1mA程度流れるようにしています。PC817のLED順方向電圧が約1.2Vなので1.2kΩになります。
R16はフォトカプラLEDの電流制限抵抗です。TL431が完全にオンしたときのカソード電圧は2.5Vです。そのため

${R_{16}=\frac{V_{out}-(2.5+1.2)}{I_{p}+I_{R_{17}}}}$

フォトカプラに流れる電流Ipは今回2mA,R17の電流IR17は1mAなのでR16=3.6kΩにしました。フォトカプラがこれでまだオンしない場合はR16を下げてみてください。

今回はPC40EI40を用いることとなりました。一次巻線を50回,二次巻線を15回,三次巻線を13回としてみました。一次電圧が100√2Vとなり二次電圧は出力電圧15Vに整流ダイオード順方向電圧1.9を加えた16.9Vとして設計してます。また出力電流I2outを最大6Aまで取り出せるように設計しています。
前回のフライバックトランスの計算式を使いました。
まず上の条件と仮定し、電圧比からデューティ比を計算します。

${D_{uty}=\frac{A_v}{\frac{N_2}{N_1}+A_v}=\frac{\frac{16.9}{100\sqrt{2}}}{\frac{15}{50}+\frac{16.9}{100\sqrt{2}}}=0.285}$

後述のデューティ比が大きくなるにつれて一次側サージ電圧も大きくなるのでデューティ比は小さめにします。少なくとも0.5以下に設定するほうがいいでしょう。
制御回路用電源の三次巻線は二次電圧より少し低めに取って、13回巻きとしました。つまり制御回路側電圧V3は

${V_3=V_2{\times}\frac{N_3}{N_2}=16.9{\times}\frac{13}{15}=14.6[V]}$

つまり14.6Vとなります。TL494やMOSFETなどをしっかり駆動できるように巻数を調整してください。制御回路の電流は0.1A程度と考えました。
ここからは最大磁束密度を考えます。

https://pccomponents.com/datasheets/TDK-E141.PDF

PC40EI40の磁路断面積Ae=148mm^2、AL値は4860nH/N^2となります。ここからコアに発生する最大磁束密度は

${B_{peak}=\frac{\frac{1}{N_1}V_1\frac{D_{uty}}{f_{osc}}+N_2A_LI_{2{out}}+N_3A_LI_{3_{out}}}{A_e}=\frac{\frac{1}{50}\times100\sqrt{2}\times\frac{0.285}{50\times10^3}+4860\times10^{-9}(15\times6+13\times0.1)}{148{\times}10^{-6}}=3.11[T]}$

PC40コアが100℃のときの飽和磁束密度が380mTでこれを優に超えてしまい、磁気飽和して大電流が流れてしまいます。そこでエアギャップlgを設けて総AL値を減らすことで発生する磁束密度を減らします。
一旦エアギャップを1mmとして総AL値のALallを計算してみると

${A_{L_{all}}=\frac{1}{\frac{1}{A_L}+\frac{l_g}{\mu_0A_e}}=\frac{1}{\frac{1}{4860\times10^{-9}}+\frac{1\times10^{-3}}{4\pi\times10^{-7}\times148\times10^{-6}}}=179[nH/N^2]}$

ALall=179nH/N^2として最大磁束密度を再計算してみると

${B_{peak}=\frac{\frac{1}{50}\times100\sqrt{2}\times\frac{0.285}{50\times10^3}+179\times10^{-9}(15\times6+13\times0.1)}{148{\times}10^{-6}}=219[mT]}$

かなり余裕ができて、さらに電流が流せるようになりました。この条件でエアギャップlg=1mmと決まりました。(もっと厳密に式を変形してエアギャップを求めたほうが、結合度が高まってサージも減るんですけどね...結構大雑把です)
MOSFETのドレインにはトランスによって大きなサージ電圧がかかります。一次側回路はブーストコンバータと見ることができます。すなわち一次側に発生するサージ電圧の最低値は

${V_{surge_{min}}=Vin{\times}\frac{1}{1-D}}$