初版

NE555で3.3V出力の降圧DC/DCコンバータを作ってみた。

製作品

(CC BY-NC-SA 4+) Creative Commons Attribution-NonCommercial-ShareAlike CC BY-NC-SA version 4.0 or later

# はじめに NE555(以下、555)の応用案として、オペアンプとLDOを組み合わせた、3.3V出力の降圧DC/DCコンバータを試作した。 以下のツイートのように、入力電圧VCCによらず出力電圧VOUTは3.3Vの一定出力を保つことができている。 @[twitter](https://twitter.com/electrotelecast/status/1505911297984311296?s=20&t=QTNIbNC8R0DX_4NtvZZuXw) 本記事では、DC/DCコンバータの基本原理と、555のCTRL端子(5pin)を用いたDuty比の制御を説明した後、実際に試作したDC/DCコンバータの回路と、その測定結果について紹介していきたい。 # 原理説明 まずは、今回作成した降圧型DC/DCコンバータの原理を説明する。 この章は、長いうえに数式による議論が多い。回路で必要な部分は後の章でも触れるので、理屈はいいから回路構成や実験結果を早く知りたい、という方は、この章を読み飛ばすことを推奨する。 ## 降圧DC/DCコンバータの原理 試作回路を紹介する前に、今回作成した降圧DC/DCコンバータの動作原理を説明する。 基本的な回路構成は、２個のスイッチとコイル、負荷コンデンサで構成される回路である。(下図) 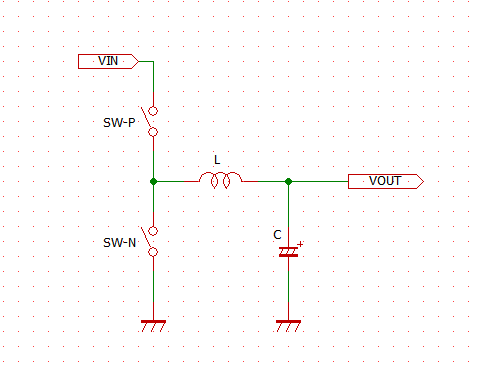 この回路により、VINに対して、スイッチのON/OFF制御(スイッチング制御)を行うことで所望の出力電圧(VOUT)を得ることができる。 以下では、VINに対してVOUTをどのように決めることができるのか、その動作とともに説明したい。 ### SW-PがON、かつ、SW-NがOFFのとき まず、上側のスイッチSW-PがONで、かつ、下側のスイッチSW-NがOFFのときのVOUT変化を考える。 このとき、VINからコイルを通じて、負荷コンデンサに電流が流入し、VOUTの電圧が上昇する。 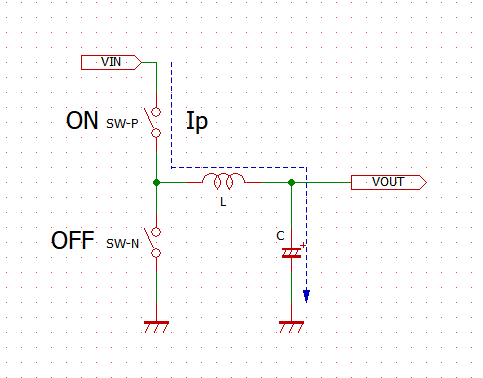 この流入電流を$I_p$とすると、$I_p$とVIN電圧$V_i$、VOUT電圧$V_o$の関係は以下のような微分方程式で表される。 $$ V_i - V_o = L \frac{dI_p}{dt}(t) $$ $V_i$と$V_o$が、SW-PがONしている時間$t_p$の間、ほぼ一定であるとすると、以下の関係が得られる。 $$ I_p = \frac{V_i - V_o}{L} t_p $$ ### SW-PがOFF、かつ、SW-NがONのとき 次に、上側のスイッチSW-PがOFFで、かつ、下側のスイッチSW-NがONのときのVOUT変化を考える。 このとき、負荷コンデンサに溜まった電荷は、コイルを通じてGNDに放電され、VOUTの電圧は低下する。 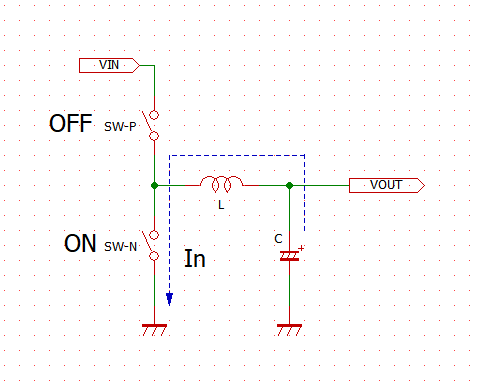 この放電電流を$I_p$とすると、$I_p$とVIN電圧$V_i$、VOUT電圧$V_o$の関係は以下のような微分方程式で表される。 $$ V_o = L \frac{dI_n}{dt}(t) $$ $V_i$と$V_o$が、SW-NがONしている時間$t_n$の間、ほぼ一定であるとすると、以下の関係が得られる。 $$ I_n = \frac{V_o}{L} t_n $$ ### VINとVOUTの関係 VOUTが一定電圧を保持していると仮定すると、負荷コンデンサに流入する電流量と、放電する電流量は等しいはずである。すなわち、$I_p = I_n$が成り立つ。先ほどの議論から、 $$ I_p = \frac{V_i - V_o}{L} t_p = \frac{V_o}{L} t_n = I_n$$ となり、これを$V_o$について解くことで、$V_o$は、 $$ V_o = \frac{t_p}{t_p+t_n} V_i = Duty \times V_i$$ と表すことができる。なお、$Duty$はスイッチング周期 $t_p + t_n$ に対する、SW-Pのオン時間 $t_p$ の比である。 ## CTRLに電圧印加した場合の555無安定モード 555をスイッチング制御に用いる前に、CTRLピン(5pin)に任意の電圧をかけた場合の無安定動作について検討する。 動作の概略については、taltalp氏の[回路シミュレータで作るNE555タイマー](https://elchika.com/article/6b627232-2a07-45c7-a923-30ff7bff4d76/)が非常に分かりやすいので、まずは一読いただきたい。 本記事では、数式を用いて発振周期を詳細に求めていきたい。なお、以下の議論は下図の回路を想定して行い、回路定数も下図のものを用いる。  OUT端子がH/Lを維持しているとき、コンデンサCは充電/放電しており、Cの端子電圧$V_c$が変化している。 この$V_c$をコンパレータで監視し、閾値電圧$V_{thH}$を超えたときOUT端子はH→Lに、閾値電圧$V_{thL}$を下回ったときL→Hに切り替わるようになっている。この閾値電圧は、CTRLの状態によって、以下のように求められる。 1. CTRL端子に何もつながっていない場合 (通常動作): $$V_{thH} = \frac{2}{3}V_{CC}, V_{thL} = \frac{1}{3}V_{CC} $$ 2. CTRL端子に任意の電圧$\alpha V_{CC}$ $(0<\alpha\leqq 1)$がかかっている場合: $$V_{thH} = \alpha V_{CC}, V_{thL} = \frac{1}{2} \alpha V_{CC} $$ OUT端子が切り替わってから再び切り替わるまでの時間、すなわち時間OUT端子がHまたはＬを維持する時間は、Cに接続している抵抗R1, R2によって決まる。ここでは、 CTRL端子に任意の電圧$\alpha V_{CC}$がかかっている場合において、OUT端子がHの時間$t_H$とLの時間$t_L$を、それぞれ求める。 ### OUT端子がHのとき 初期状態でOUT端子がHである場合を考える。この時、$V_c$の変化は、以下のように表せる。 $$ V_c(t) = V_{CC} \Big[1-\exp \Big( -\frac{t-t_0n}{(R_1+R_2)C} \Big) \Big] $$ ただし、$t_0n$は、$V_c(t_0n) = 0$となる時刻とする。 OUT端子がL→H, H→Lに切り替わる時刻をそれぞれ$t_{rise}$, $t_{fall}$とおくとき、 $$ V_c(t_{fall}) = V_{CC} \Big[1 - \exp \Big( -\frac{t_{fall}-t_{0n}}{(R_1+R_2)C} \Big) \Big] $$ $$ V_c(t_{rise}) = V_{CC} \Big[1 - \exp \Big( -\frac{t_{rise}-t_{0n}}{(R_1+R_2)C} \Big) \Big] $$ と表せることから、 $$ t_{fall} = (R_1+R_2)C \ln \frac{ V_{CC} }{V_{CC} - V_c(t_{fall}) } $$ $$ t_{rise} = (R_1+R_2)C \ln \frac{ V_{CC} }{V_{CC} - V_c(t_{rise}) } $$ となる。したがって、OUT端子がHである時間$t_H$は、 $$ t_H = t_{fall} - t_{rise} = (R_1+R_2)C \ln \frac{ V_{CC} }{V_{CC} - V_c(t_{fall}) }\frac{ V_{CC} - V_c(t_{rise}) }{V_{CC} } $$ と書ける。ここで、条件より$V_c(t_{fall}) = V_{thH} = \alpha V_{CC}$、$V_c(t_{fall}) = V_{thH} = \alpha V_{CC}/2$となることから、 $$ t_H = (R_1+R_2)C \ln \frac{ V_{CC} }{V_{CC} -\alpha V_{CC} }\frac{ V_{CC} - \alpha V_{CC}/2 }{V_{CC} } $$ $$ \therefore t_H = (R_1+R_2)C \ln \Big( \frac{1}{2} \cdot \frac{ 2-\alpha }{1 - \alpha } \Big) $$ と表すことができる。 ### OUT端子がLである時間 初期状態でOUT端子がLである場合を考える。OUT端子がHの時と同様、OUT端子がL→Hに切り替わる時刻を$t_{rise}$、OUT端子がH→Lに切り替わる時刻を$t_{fall}$とおくと、$V_c$の変化は以下のように表せる。 $$ V_c(t) = V_c(t_{fall}) \exp \Big( -\frac{t-t_{fall}}{R_2C} \Big) $$ このとき、時刻$t_{rise}$におけるCの電圧$V_c(t_{rise})$は、 $$ V_c(t_{rise}) = V_c(t_{fall}) \exp \Big( -\frac{t_{rise}-t_{fall}}{R_2C} \Big) $$ と表せることから、OUT端子がLである時間$t_L$は、 $$ \exp \Big( -\frac{t_{rise}-t_{fall}}{R_2C} \Big) = \frac{ V_c(t_{rise}) }{ V_c(t_{fall}) } $$ $$ \therefore t_L = t_{rise}-t_{fall} = R_2C \ln \frac{ V_c(t_{fall}) }{ V_c(t_{rise}) } $$ と書ける。OUT端子がＨの時と同様、$V_c(t_{fall}) = V_{thH} = \alpha V_{CC}$、$V_c(t_{fall}) = V_{thH} = \alpha V_{CC}/2$であるので、 $$ t_L = t_{rise}-t_{fall} = R_2C \ln \frac{ V_{CC} }{ V_{CC}/2 } = R_2C \ln 2 $$ と表される。 ### OUT端子のDuty比 以上をまとめると、CTRL端子に電圧$\alpha V_{CC}$をかけたとき、OUT端子がH/Lを維持する時間は $$ t_H = (R_1+R_2)C \ln \Big( \frac{1}{2} \cdot \frac{ 2-\alpha }{1 - \alpha } \Big) $$ $$ t_L = R_2C \ln 2 $$ となり、CTRL端子の電圧を上げると$t_H$が長くなり、OUT端子がHになる時間のみが長くなる。 また、発振周期$Tは、 $$ T = t_H + t_L = (R_1+R_2)C \ln \Big( \frac{1}{2} \cdot \frac{ 2-\alpha }{1 - \alpha } \Big) + R_2C \ln 2 $$ と表され、周期$T$に対するL時間のDuty比$D_L$は、 $$ D_L = \frac{t_L}{T} = \frac{ R_2C \ln 2}{ (R_1+R_2)C \ln \Big( \frac{1}{2} \cdot \frac{ 2-\alpha }{1 - \alpha } \Big) + R_2C \ln 2}$$ と表すことができる。 # 555によるDC/DCコンバータ ここまで長々と議論してきたが、555で降圧DC/DCコンバータを作るうえで重要なのは、以下の2点である。 - 降圧型DC/DCコンバータの出力電圧$V_o$は、入力電圧$V_i$とスイッチング制御のDuty比で以下のように表される。 $$ V_o = \frac{t_p}{t_p+t_n} V_i = Duty \times V_i$$ - 555のCTRL端子に任意の電圧$\alpha V_{CC}$を入力すると、周期$T$に対するL時間のDuty比$D_L$は以下のように表される。 $$ D_L = \frac{t_L}{T} = \frac{ R_2C \ln 2}{ (R_1+R_2)C \ln \Big( \frac{1}{2} \cdot \frac{ 2-\alpha }{1 - \alpha } \Big) + R_2C \ln 2}$$ これらを用いることで、555を用いた降圧型DC/DCコンバータを組むことができる。 以下では、作成した回路とその測定結果を紹介していく。 ## 可変抵抗による任意の電圧出力 まずは、CTRL端子に任意の電圧をかけられるよう、ボリュームを用いた回路で実験を行った。 555による発振回路、555のCTRLの電圧調整用のボリューム、電圧出力のためのSW (MOSFET)、コイル、負荷コンデンサで構成している。(下図) 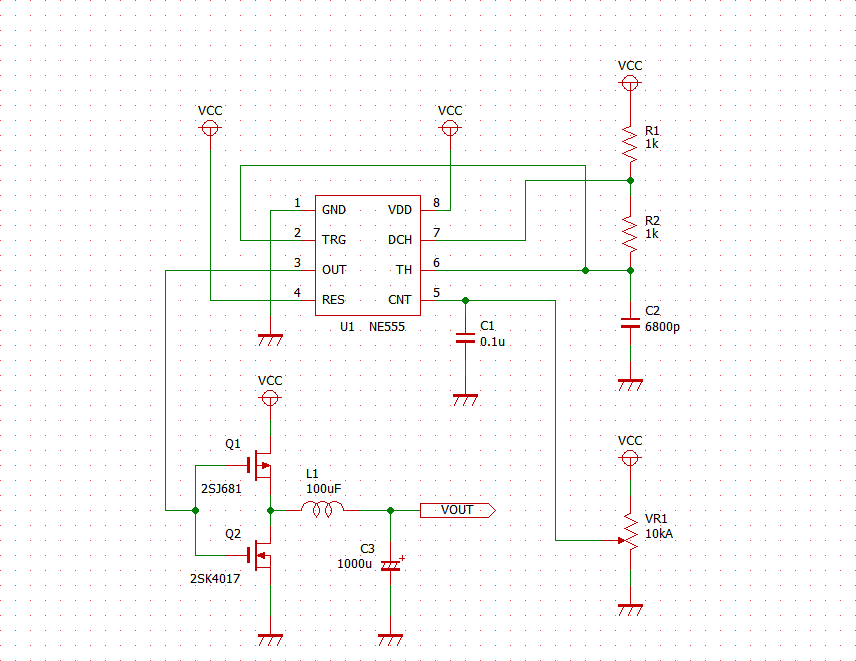 上記の回路により、可変抵抗でCTRL端子にかかる電圧を変えることで、下記ツイートのようにDC/DCの出力電圧Voutを変えることができた。 なおツイートの画像は、1枚目は測定環境を、2～4枚目がCTRL電圧を変えたときのVOUTの変化を示しており、2~4枚目の波形は、水色がDC/DCコンバータの出力Voutの、黄色が555のOUT端子電圧の時間変化を表している。 @[twitter](https://twitter.com/electrotelecast/status/1505591444404596737?s=20&t=QTNIbNC8R0DX_4NtvZZuXw) この構成により、CTRL端子の電圧を変えることにより、発振のDuty比を変えることができ、出力電圧をVoutを変えることができた。 しかしこの回路は、2つの改善点が存在する。 1. ボリュームの位置を固定している状態でVCCが変化したとき、出力電圧Voutも連動して変化する。 すなわち、入力安定度が悪い。 2. 出力Voutに抵抗値の低い負荷を接続すると、負荷に流れる電流によって出力電圧も連動して変化する。 すなわち、負荷安定度が悪い。 これらは、DC/DCコンバータの主な用途である安定化電源として用いる場合には、とても都合が悪い。 なぜなら、安定化電源の用途はそもそも、入力電圧の変動や出力電流の変動に対して、出力が変動してほしくない機器の電源だからである。 ## フィードバックによる出力電圧安定化 ### 回路説明 上記の改善点を解決する方法の一つとして、出力電圧Voutの変化を読み取り、それに応じてスイッチング制御のDuty比を変える、フィードバック制御が挙げられる。このフィードバックを実現するために、オペアンプと、LDOによる基準電圧を追加した。(下図) 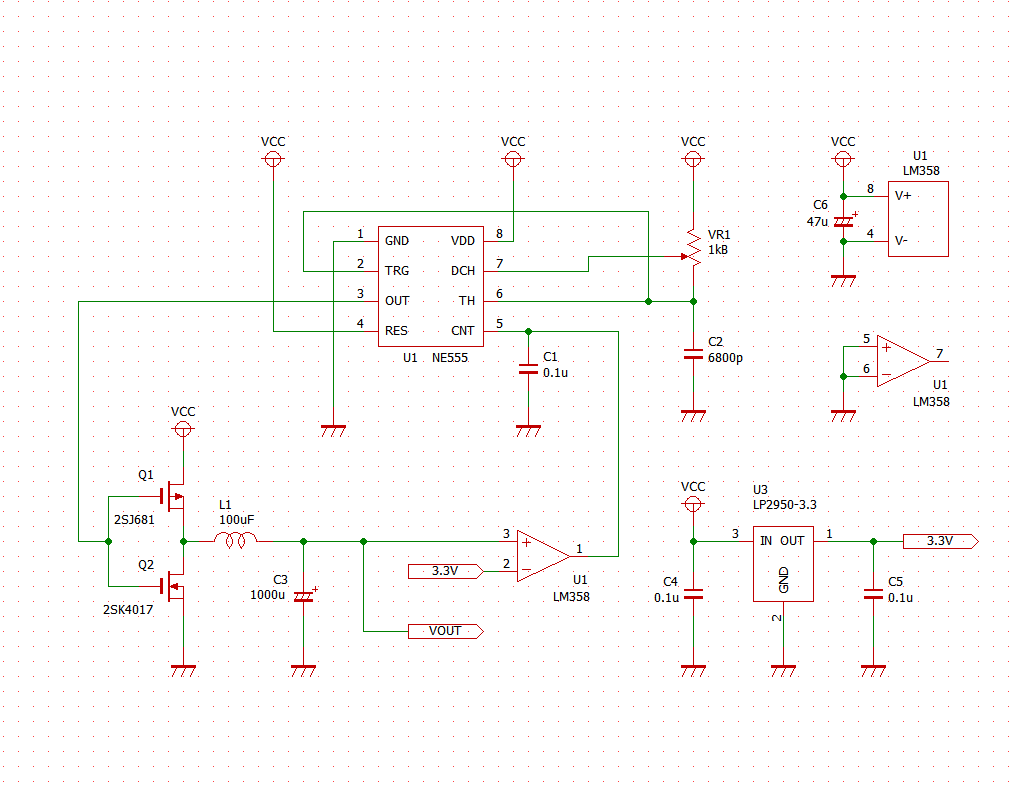 この回路追加により、Voutが上昇した場合は、その上昇量に応じてCTRLの電圧を上げることで、Duty比$D_L$を下げ、上がったVoutを下げようとし、Voutが低下した場合は上昇時と逆に下がったVoutを上げようとすることで、Voutを一定に保つことができる。このフィードバックループを作ることにより、この時VoutはオペアンプのV+とV-の電圧が一致させるように制御が働き(イマジナリーショート)、3.3Vに保たれる。 実際、この構成でDC/DCの出力Vout(水色)と555のOUT端子の電圧(黄色)の出力を確認すると、Voutの変化に対してOUT端子の発振周波数が変化していることがわかる。 @[twitter](https://twitter.com/electrotelecast/status/1505907962212405253?s=20&t=QTNIbNC8R0DX_4NtvZZuXw) なお、CTRL端子の電圧が変わるとDuty比が変わると説明したが、実際にはOUT端子がHになっている時間$t_H$だけである(DC/DCの動作としてはSW-Nのオン時間のみが伸びる)。 このため、この制御は、Duty比だけでなく動作周波数$1/T$も変化する、PFM(Pulse Frequency Modulation)制御である。 ### 出力電圧の安定性測定 上記の改善点で上げた、入力電圧と出力負荷の変化に対するVoutの安定性を確認結果を以下に示す。 #### ① 入力電圧の変化に対する出力電圧 (入力安定度) 入力電圧VCCを5V, 7.5V, 10V, 12Vに変えたときの出力電圧Voutの変化を以下に示す(いずれの条件においても、負荷抵抗なし)。いずれの波形も、入力電圧VCCを水色、出力電圧VOUTを黄色で示している。入力電圧が上がると、出力電圧の揺れが大きくなるものの、おおよそ3.3Vを保持できていることがわかる。 |  | 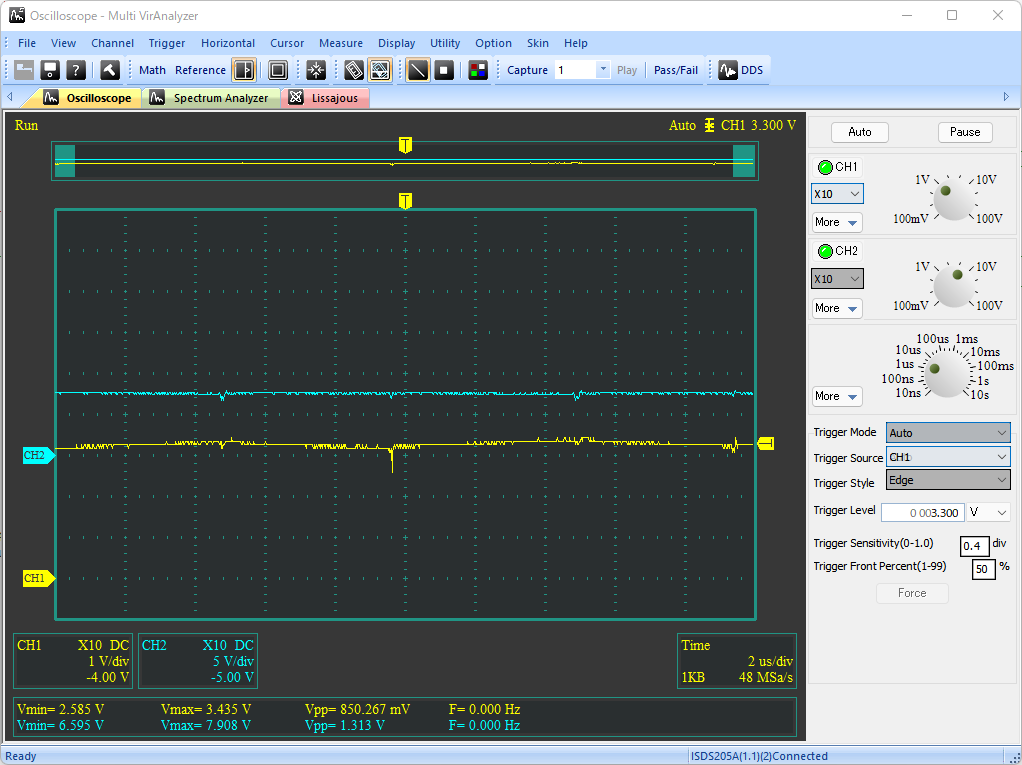 | |:---:|:---:| |  | 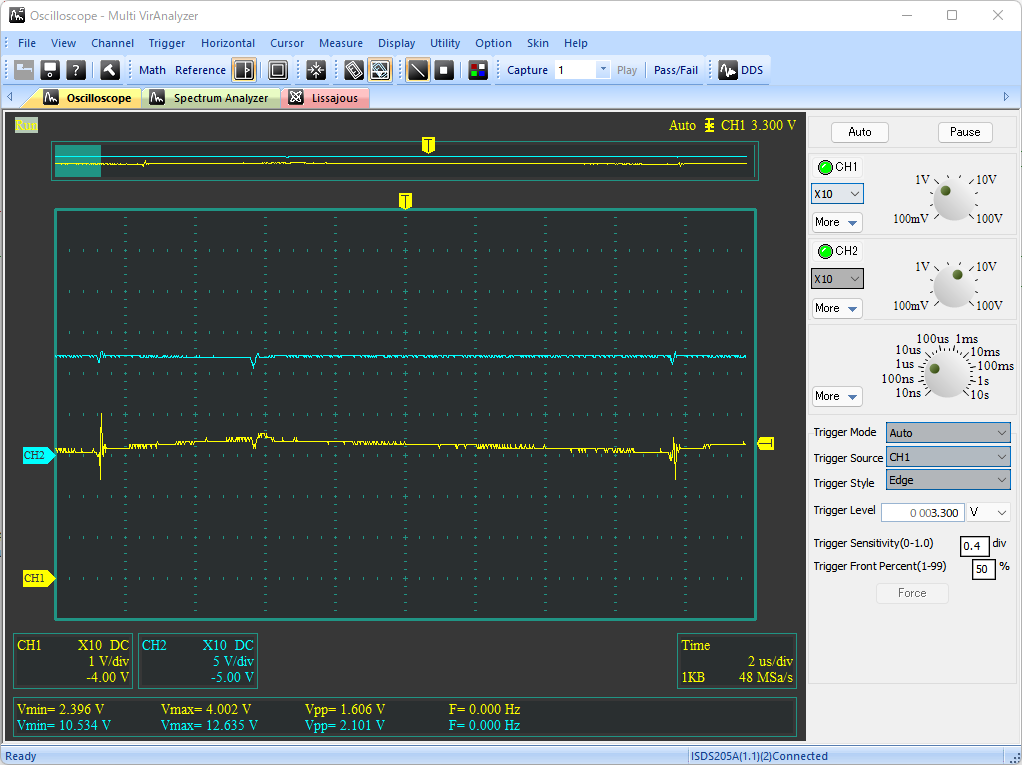 | #### ② 出力負荷の変化に対する出力電圧 (負荷安定度) 出力負荷を無負荷, 1kΩ, 220Ω, 20Ωに変えたときの出力電圧Voutの変化を以下に示す(いずれの条件においても、VCC=5V)。いずれの波形も、入力電圧VCCを水色、出力電圧VOUTを黄色で示している。入力電圧の変化と異なり、出力負荷の抵抗値が変わってもVoutの揺れはほとんど変わらないことがわかる。 | 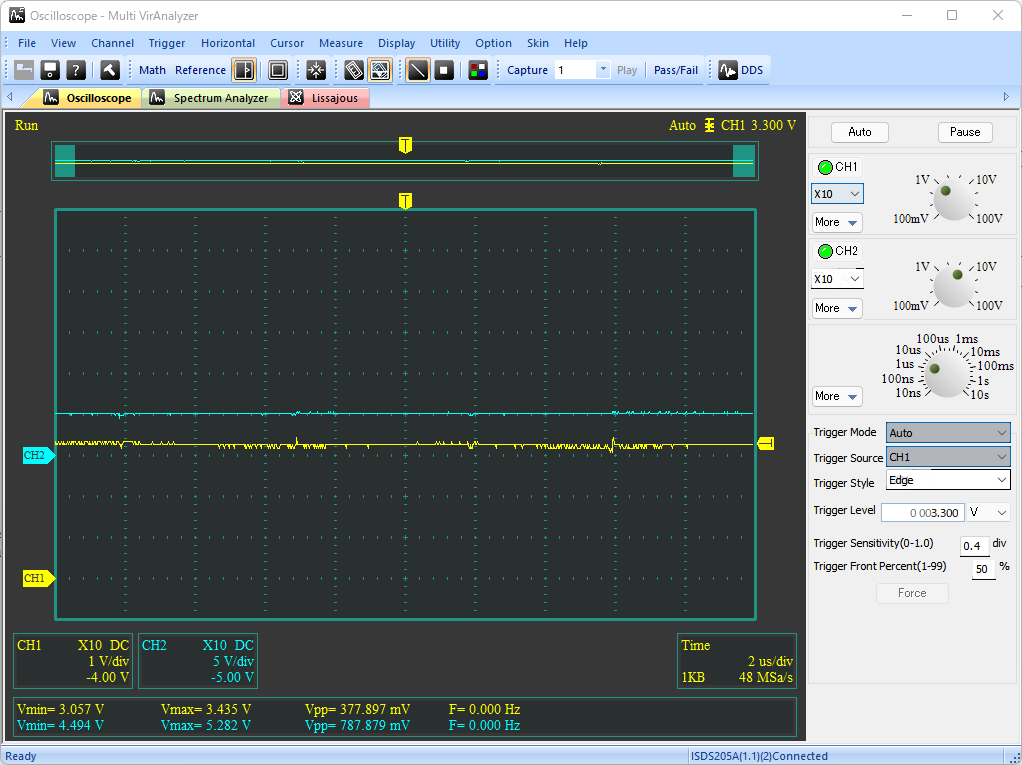 | 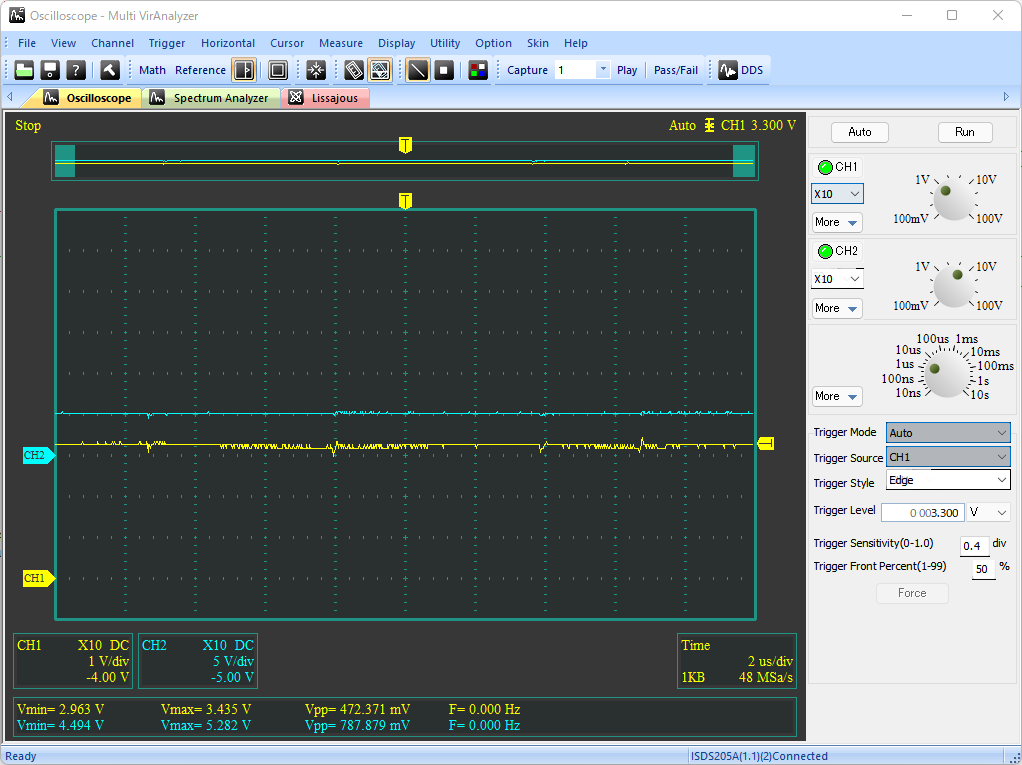 | |:---:|:---| | 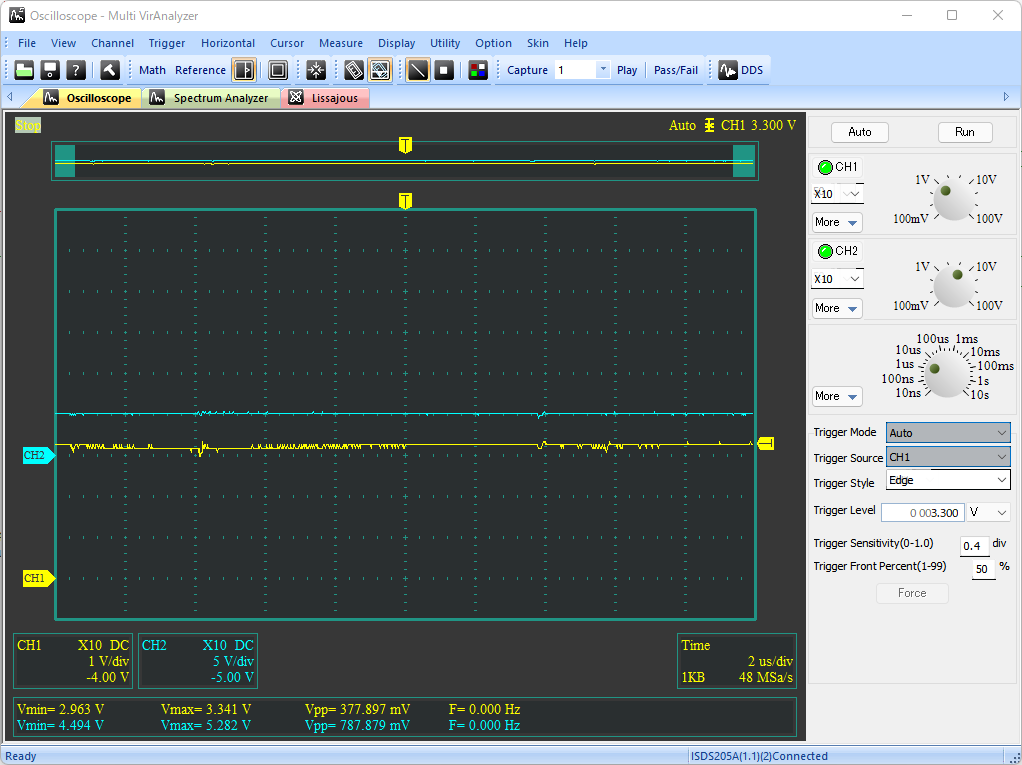 | 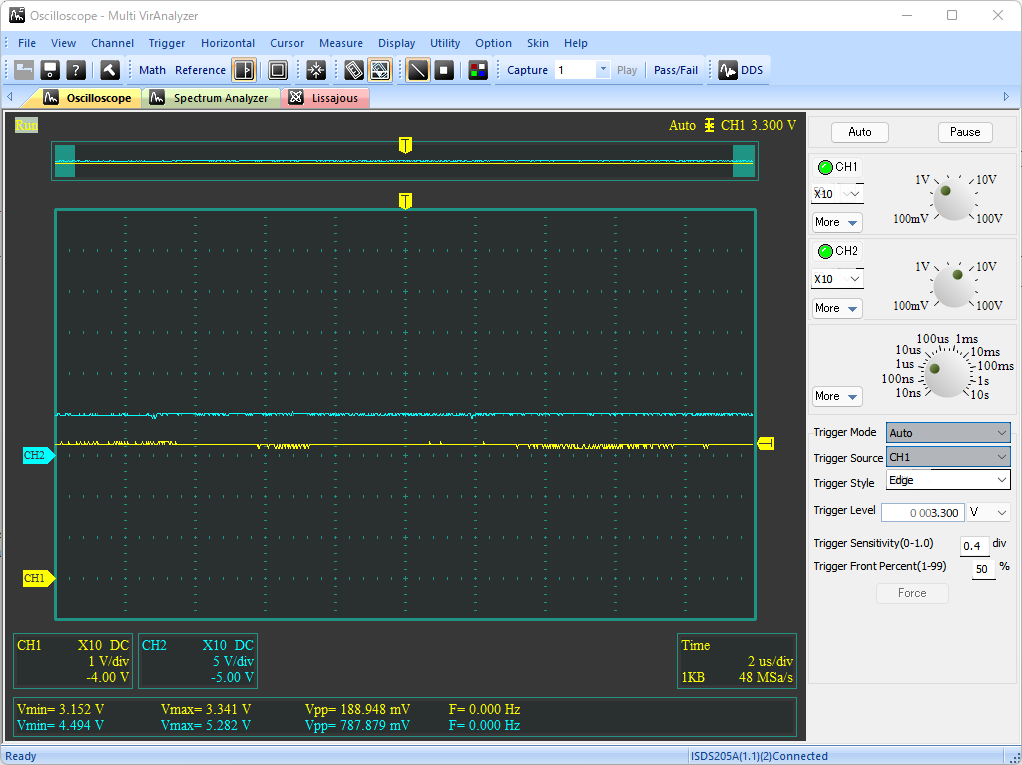 | # まとめ 以上のように、555とオペアンプを組み合わせることで、入力・出力の状態によらず一定出力を保つ、降圧DC/DCコンバータの実現に成功した。 最後に、今回の達成事項のまとめと、今後の課題を示す。 ==達成できたこと 入力電圧や負荷によらず、一定の出力電圧を保つことのできる、降圧DC/DCコンバータを設計・試作できた。== ++今後の課題 ・出力電圧を自在に変更すること。(今回は電圧源の電圧3.3Vしか出力できない) ・PFM制御を効果的に行うには、可変抵抗VR1を適切に調整する必要があること。(調整なしで発振周波数を決めたい)++