エミッタ接地増幅回路の交流等価回路の実測

本記事ではエミッタ接地増幅回路の各種特性を実測し、交流等価回路と比較します。

背景

「例解アナログ電子回路」という本でエミッタ接地増幅回路の交流等価回路を学びました。ただ、その等価回路が本物の回路の動作をきちんと表せていることが、いまいちピンと来ませんでした。そこで、実際に回路を組み、各種の特性を実測し、等価回路と比較してみることにしました。

実験の対象にした回路はこれです。

部品定数は次の通りです。

等価回路は何故登場するのでしょう？筆者の理解は、R、L、C という受動部品だけからなる回路に変換することで、各種の計算が簡単になる、ということです。例えば、このエミッタ接地増幅回路の入力インピーダンスを計算するにあたり、元々の回路では計算が複雑になります。特にトランジスタを計算に組み込むのがかなり難しそうです。もし、回路が R、L、C だけで表せれば、インピーダンスの計算はぐっと簡単になります。

直流等価回路

等価回路には「直流等価回路」と「交流等価回路」の 2 種類があるようです。直流等価回路は入力信号が 0 の場合の回路、交流等価回路は直流成分を無視した場合の回路です。回路を流れる信号を直流と交流の重ね合わせだと考え、直流と交流を別々に計算することで、容易に解析ができるようになります。理科の授業で習う波の重ね合わせと同じような感じで、電気信号においても重ね合わせとして考えることができるわけです。

さて、上で示したエミッタ接地増幅回路の直流等価回路を考えます。直流ではコンデンサは電気を通さないため開放除去します。得られる回路は次のようになります。

各点に発生する電圧と電流を求めたいです。直流での電圧、電流のことを動作点と言います。実際に回路の電圧を測れば分かりますが、まずは机上で計算してみます。その後、計算値と実測値を比較してみます。

動作点の計算

使用したトランジスタは UTC 製の 2SC1815 で、ランクは GR です。GR では直流電流増幅率 hFE は 200～400 です。仮に hFE=300 とします。つまり

$I_c=h_\mathrm{FE}\times I_b$

キルヒホッフの電流則より

$I_e=I_b+I_c$

$I_{R_2}=I_b+I_{R1}$

以上から、$a=1+h_\mathrm{FE}$とおくと

$I_e=I_b+h_\mathrm{FE}\times I_b=aI_b=a(I_{R_2}-I_{R1})$

R1、Q1のベース、エミッタ、Reのループにおいて、キルヒホッフの電圧則より

$R_1I_{R_1} = V_\mathrm{BE}+R_eI_e$

$I_e=a(I_{R_2}-I_{R1})$を代入して整理すると

$(R_1+aR_e)I_{R_1}=V_\mathrm{BE}+aR_eI_{R_2}$

オームの法則より

$R_1I_{R_1}+R_2I_{R_2}=5$

連立方程式を解くと

$I_{R_1}=\frac{V_\mathrm{BE}R_2+5aR_e}{R_1R_2+aR_e(R_1+R_2)}$

トランジスタのベース・エミッタ間電圧$V_\mathrm{BE}$は大体 0.7V となることが知られています。部品の数値を用いて計算すると

$I_{R_1} \approx 19.5 \mathrm{\, \mu A}$

したがって

$I_{R_2}=\frac{5-R_1I_{R_1}}{R_2} \approx 60.8 \mathrm{\, \mu A}$

$I_b=I_{R_2}-I_{R_1} \approx 41.3 \mathrm{\, \mu A}$

$I_e=aI_b=12.4 \mathrm{\, mA}$

動作点の実測

無信号時の各点の電圧を測定すると次の通りとなりました。「電圧」の列は実測値で、「電流」の列は電圧と抵抗値から計算で求めた値です。

先ほど計算で求めた値と近い値が得られました。R1、R2 の電流を用いて計算すると $I_b=45.01 \mathrm{\, \mu A}$であることが分かります。

教科書のバイアス抵抗計算式の罠

「例解アナログ電子回路」p.49 に、バイアス抵抗（R1、R2）を決めるための式が載っています。

R1～トランジスタのベース～トランジスタのエミッタ～RE～R1のループを考えると、

$\frac{R_1}{R_1+R_2}\dot{V}\!_{CC}=\dot{V}\!_{BE}+R_E\frac{\dot{V}\!_{CC}}{2(R_C+R_E)}$

とのことです。この式の左辺は VCC を R1 と R2 で分圧した電圧を表します。しかし、これはベース電流を無視してしまっています。ベース電流が 0 であれば抵抗分圧はこの式で正しいのですが、ベース電流が流れる場合、R2 に流れる電流が R1 の電流より多くなり、分圧された電圧は抵抗比の通りではなくなります。

ベース電流による R2 の電圧降下分が無視できるほど小さければ良いのですが、現実には Ib=Ic/hFE くらいのベース電流が必要です。Ic=10mA、hFE=300 とすると、Ib=33uA 程度となります。従って、R2 の電圧降下は 33uA×R2 となります。R2=1kΩ で 33mV、R2=10kΩ で 0.33V、R2=100kΩ で 3.3V ということです。0.33V 程度としても、無視できるとは言えないと筆者は感じました。

また p.52 では「R1//R2 >> hie である場合には」とあるように、R1 と R2 は hie と比べて非常に大きな抵抗を選ぶのが普通です。後で測定するのですが、hie は大体 1kΩ 程度ですから、少なくとも R1 と R2 は 10kΩ やそれより大きな値を選ぶ必要があるわけです。十分に大きな値として、100kΩ くらいを選びたいところです。「定本 トランジスタ回路の設計」の第 2 章の最初に紹介されるエミッタ接地増幅回路では、R1=22kΩ、R2=100kΩ^[1]としています。VCC=15V なので直接の比較はできませんが、やはりこのくらい大きな抵抗を使うのが典型的な設計だと言えるでしょう。

仮に R2=100kΩ を選ぶと電圧降下は 3.3V にもなって、これは VCC=5V からすると誤差では済まない電圧です。ですから、p.49 に掲載されている数式では、上手く R1 と R2 を選ぶことはできません。「定本 トランジスタ回路の設計」p.35 でも「トランジスタに流れ込むベース電流の直流成分 IB は小さいので無視すると」という記述があり、簡易的な設計では IB=0 と「近似」することになっています。筆者は、この近似は精度が全然良くないなあと思うのですが、皆さんはどう感じますか？

ちなみに、上記の数式で今回作った回路の Vb を求めると

$\frac{R_1}{R_1+R_2}\dot{V}\!_{CC}=\frac{100.0\mathrm{\, k\Omega}}{100.0\mathrm{\, k\Omega}+50.2\mathrm{\, k\Omega}}\times 5\mathrm{\, V}=3.329\mathrm{\, V}$

となり、実測値の 1.796V とは大きく異なります。

交流等価回路

交流等価回路は直流成分を無視し、交流成分だけを考えた等価回路です。先ほど求めた動作点に、交流等価回路で求める交流信号を足し合わせることで、実際の回路の電圧や電流が求まります。

「例解アナログ電子回路」p.42 より、交流等価回路を求める際の直流電源、コンデンサは次の通り処理します。

1. 直流電源には交流小信号が存在しないので、直流電源を短絡する。
2. コンデンサは、直流ではインピーダンスが無限大であるが、交流ではコンデンサの容量が非常に大きいと仮定して、インピーダンスが0と見なす。従って、交流小信号解析においても、コンデンサは短絡と見なす。
3. 同じ電位となるところは、まとめるようにする。
4. トランジスタを図 3.2 に示すような h パラメータ等価回路を用いて置き換える。

この通りに交流等価回路を作ってみます。まず 1、2 の処理をした回路は次のようになります。

3 の処理を行うと次のようになります。「R1//R2」は抵抗 R1 と R2 の並列接続を意味します。「RL//Rc」も同様に並列接続の意味です。

最終的な交流等価回路を次に示します。

エミッタ接地の場合の h パラメータは次の 4 つです。（「例解アナログ電子回路」p.25 より）

• hie: 出力端短絡入力インピーダンス
• hre: 入力端開放期間電圧利得
• hfe: 出力端短絡電流利得
• hoe: 入力端開放出力アドミタンス

このなかで hfe は良く見かけるのではないでしょうか。先ほどの動作点の計算で出てきた hFE の交流版で、交流信号における電流の増幅率を表します。実際の解析では hre と hoe はほぼゼロとなり、無視できるそうですので、上記の等価回路ではそれらは省略しています。

入出力インピーダンスの計算

ここでは Rin は入力信号 Vin の内部抵抗ということにして、それより右側のインピーダンスを入力インピーダンスと考えることにしましょう。すると R1、R2、hie の並列接続ですから、入力インピーダンス Zin は次のように計算できます。

$Z_{in}=R_1//R_2//h_{ie}$

hie の値が不明なので、これ以上計算ができませんね。後回しにして、先に出力インピーダンスを求めます。

出力インピーダンスは RL より左側のインピーダンスですので

$Z_{out}=R_c=148.5\mathrm{\, \Omega}$

出力インピーダンスの測定

出力インピーダンスは h パラメータが関与せず^[2]値が求まっているので、実際の値を測定して等しいか検証してみようと思います。RL を開放除去したときと RL を付けたときの出力電圧から、出力インピーダンスを求めることができます。

まず RL を開放除去したときの出力電圧を測定すると、Vout=1.7851Vp-p です。これを V0 としましょう。

次に RL=982 として出力電圧を測定すると、Vout=1.5463Vp-p です。V1 とします。

テブナンの定理を用いると、出力の部分は上図の回路と等価です。したがって

$V_1=\frac{R_L}{Z_0+R_L}V_0$

より

$Z_0=\frac{V_0-V_1}{V_1}R_L=151.65\mathrm{\, \Omega}$

交流等価回路に基づいた計算値とほぼ等しい値となりました。めでたしめでたし。

入力インピーダンスの計算と測定

さて、後回しにしていた入力インピーダンスを計算し、その後測定により正しさを確認してみたいと思います。

hie の決定

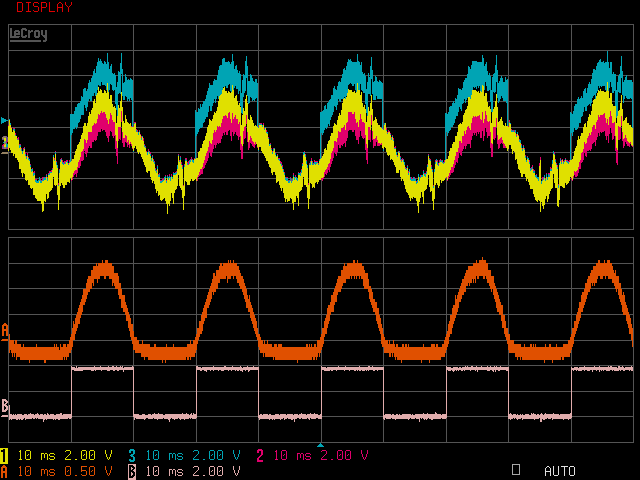
入力インピーダンスを計算するためには hie の値を求めなければいけません。hie はベース電圧の変化量をベース電流の変化量で割れば求めることができます。ということで、Vb、Ib を計測しました。

Vb はベース端子にオシロスコープを接続して計測できます。Ib は直接的な計測ができませんので、Rin、R1、R2 に流れる電流を用いて、キルヒホッフの電流則より計算した値を用います。$I_b=I_{in}+I_{R_2}-I_{R_1}$となります。図の Ib がその計算結果のグラフです。

$h_{ie}=\frac{\Delta V_b}{\Delta I_b}=\frac{51.636\mathrm{\, mV}}{47.664\mathrm{\, \mu A}}=1083.3\mathrm{\, \Omega}$

入力インピーダンスの計算

hie が求まったので、改めて入力インピーダンスを計算すると

$Z_{in}=R_1//R_2//h_{ie}=1049.3\mathrm{\, \Omega}$

簡易な解析では、hie は R1=100.0 kΩ、R2=50.2 kΩ より十分小さいので、$R_1//R_2//h_{ie}\approx h_{ie}$と近似することができます。

入力インピーダンスの測定

入力インピーダンスが 1049.3Ω と求まりましたので、実際に測定して等しいか検証します。

Rin は信号源の内部抵抗と考えていますので、エミッタ接地回路からみた入力電圧は Cin の負極の電圧 V_Cin- ということになります。オシロスコープの観測結果より、V_Cin-=48.06mVp-p です。また、入力電流は Rin の両端の電圧を用いて計算できます。Iin=54.03uAp-p となりました。

従って、エミッタ接地回路の入力インピーダンスは

$Z_{in}=\frac{\Delta V_{C_{in-}}}{\Delta I_{in}}=\frac{48.06\mathrm{\, mV}}{54.03\mathrm{\, \mu A}}=889.51\mathrm{\, \Omega}$

計算値と大きくは外れていませんが、少しずれてしまいました……

まとめ

直流等価回路、交流等価回路ともに、計算値と実測値に大きな乖離はありませんでした。多少のずれは観測されましたが、簡易な設計では無視していい差だと感じます。筆者としては、hie の値が約 1kΩ 程度だということが分かったことが、かなりの収穫となりました。

---

1. 抵抗の番号は「例解アナログ電子回路」に合わせて変更している。 ↩︎

2. hfe はインピーダンス計算に無関係で、hoe は無視しているため。 ↩︎