初版

ラプラス変換による電気回路解析 - RC, RLフィルタ

これの続き Wolfram Engine + Jupyter notebookで回路解析 (Windows) | elchika https://elchika.com/article/ef587a27-9e1e-4c10-820d-070477c3cb1f/ ## 前書き ラプラス変換はコンピュータで計算できるため非常に便利ではありますが、割と一長一短なところがあります。 * ラプラス変換の長所 コンピュータに解かせる事ができる。 フェーザ法では適応できない交流以外の入力に対して対応できる。 * ラプラス変換の短所 コンデンサに電荷が蓄えられている状態を解析するのが困難。 コンデンサに電荷が蓄えられている状態を解析するのは微積のほうが楽です。 これは、コンデンサが含まれる回路では電荷に関する微分方程式を解くため、電荷の初期条件を適用するのが容易（というか必須）だからです。 ゆえに、初期条件でコンデンサの電荷が０となっている状態の回路でないと解析は難しいです。 今回はラプラス変換を用いると瞬で解ける例としてフィルタ回路を紹介します。いずれもコンデンサの電荷は初期状態で0とします。 復習ですが、ラプラス変換によるs関数を用いたインピーダンスは次のようになります。 * 抵抗: $R$ * コイル: $sL$ * コンデンサ: $\frac{1}{sC}$ ## "RR"フィルタ 今回はRC, CR, RLフィルタを解析していきますが、その前に"RR"である状態を考えます。 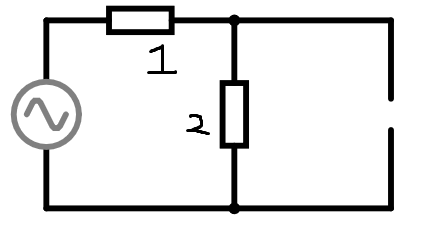 この時、出力される電圧$V_{OUT}$を考えてみると、分圧抵抗から $$V_{OUT}=\frac{R_2}{R_1+R_2}V_{IN}$$ となります。以降のフィルタ回路は全部分圧抵抗と同じ考え方となります。 ## ローパスRCフィルタ  $$\mathcal{L}[V_{OUT}]=\frac{\frac{1}{sC}}{R+\frac{1}{sC}}\mathcal{L}[V_{IN}]=\frac{1}{sCR+1}\mathcal{L}[V_{IN}]$$ 入力電圧$V_{IN}= cos(\omega t)$とすると、 $$\mathcal{L}[V_{OUT}]=\mathcal{L}[cos (\omega t)]= \frac{s}{s^2+\omega ^2}$$ よって、 $$\mathcal{L}[V_{OUT}]=\frac{1}{sCR+1}\frac{s}{s^2+\omega ^2}$$ 逆ラプラス変換を行い、 $$V_{OUT}=\frac{cos(\omega t)+\omega CR sin(\omega t)-e^{-\frac{t}{CR}}}{\omega^2C^2R^2+1}$$ 定常解は $$V_{OUT}=\frac{cos(\omega t)+\omega CR sin(\omega t)}{\omega^2C^2R^2+1}$$ $C=100nF, R=1k\Omega$として周波数特性をプロットすると次のようにローパスである事がわかる。 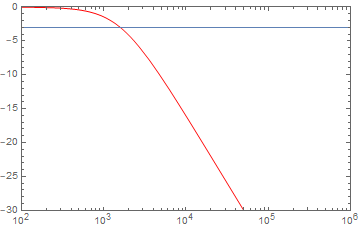 カットオフ周波数は $$f_{0}=\frac{1}{2\pi CR}=\frac{1}{2\pi\times 10^{-7}\times 1000}=1592 Hz$$ ## ハイパスCRフィルタ  $$\mathcal{L}[V_{OUT}]=\frac{R}{R+\frac{1}{sC}}\mathcal{L}[V_{IN}]=\frac{sCR}{sCR+1}\mathcal{L}[V_{IN}]$$ 入力電圧$V_{IN}= cos(\omega t)$とすると、 $$\mathcal{L}[V_{OUT}]=\mathcal{L}[cos (\omega t)]= \frac{s}{s^2+\omega ^2}$$ よって、 $$\mathcal{L}[V_{OUT}]=\frac{sCR}{sCR+1}\frac{s}{s^2+\omega ^2}$$ 逆ラプラス変換を行い、 $$V_{OUT}=\frac{\omega ^2 C^2R^2 cos(\omega t) - \omega CR sin(\omega t)+e^{-\frac{t}{CR}}}{\omega^2C^2R^2+1}$$ 定常解は $$V_{OUT}=\frac{\omega ^2 C^2R^2 cos(\omega t) - \omega CR sin(\omega t)}{\omega^2C^2R^2+1}$$ $C=100nF, R=1k\Omega$として周波数特性をプロットすると次のようにハイパスである事がわかる。  カットオフ周波数は $$f_{0}=\frac{1}{2\pi CR}=\frac{1}{2\pi\times 10^{-7}\times 1000}=1592 Hz$$ ちなみに先ほどのローパスRCフィルタと周波数特性をあわせるとこんなかんじになる。 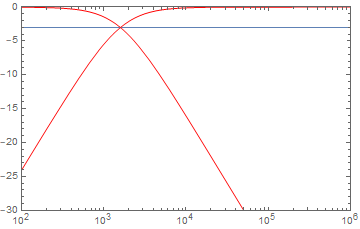 ## ハイパスRLフィルタ  $$\mathcal{L}[V_{OUT}]=\frac{sL}{R+sL}\mathcal{L}[V_{IN}]$$ 入力電圧$V_{IN}= cos(\omega t)$とすると、 $$\mathcal{L}[V_{OUT}]=\mathcal{L}[cos (\omega t)]= \frac{s}{s^2+\omega ^2}$$ よって、 $$\mathcal{L}[V_{OUT}]=\frac{sL}{R+sL}\frac{s}{s^2+\omega ^2}$$ 逆ラプラス変換を行い、 $$V_{OUT}=\frac{L^2 \omega ^2 cos (\omega t)-RL \omega sin (\omega t) + R^2e^{-\frac{Rt}{L}} }{R^2+L^2 \omega ^2}$$ 定常解は $$V_{OUT}=\frac{L^2 \omega ^2 cos (\omega t)-RL \omega sin (\omega t)}{R^2+L^2 \omega ^2}$$ $L=100mH, R=1k\Omega$として周波数特性をプロットすると次のようにハイパスである事がわかる。  カットオフ周波数は $$f_{0}=\frac{R}{2\pi L}=\frac{1000}{2\pi \times 100 \times 10^{-3}}=1592 Hz$$ $L=100mH, R=1k\Omega$のハイパスRLフィルタと、$C=100nF, R=1k\Omega$のハイパスCRフィルタは殆ど同じ周波数特性を持つ。（実際にプロットして確認してみてください） ローパスLRも同じような感じで解くので省略。 ## おまけ: LCで作るとどうなるか つまりこういう回路 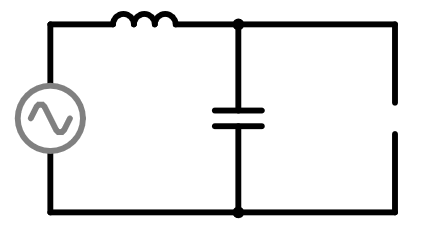 $$\mathcal{L}[V_{OUT}]=\frac{\frac{1}{sC}}{sL+\frac{1}{sC}}\mathcal{L}[V_{IN}]=\frac{1}{s^2LC+1}\mathcal{L}[V_{IN}]$$ 入力電圧$V_{IN}= cos(\omega t)$とすると、 $$\mathcal{L}[V_{OUT}]=\mathcal{L}[cos (\omega t)]= \frac{s}{s^2+\omega ^2}$$ よって、 $$\mathcal{L}[V_{OUT}]=\frac{1}{s^2LC+1}\frac{s}{s^2+\omega ^2}$$ 逆ラプラス変換を行い、 $$V_{OUT}=\frac{cos(\frac{t}{\sqrt {LC}})-cos (\omega t)}{LC \omega ^2-1}$$ これはそのまま定常解なので$L=100mH, C=100nF$として周波数特性をプロットすると次のように出力される。 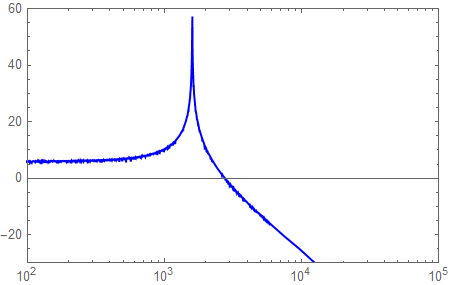 ただしこの回路は自己発振するためきれいな正弦波を出力しません。回路シミュレータで実際に制作してみてください。 共振周波数は $$f_{0}=\frac{1}{2\pi \sqrt {LC}}=\frac{1}{2\pi \sqrt {100 \times 10^{-3} \times 100 \times 10^{-9}}}=1592 Hz$$ また、この回路に直流1Vを入力した場合、すなわち $$\mathcal{L}[V_{OUT}]=\frac{1}{s^2LC+1}\frac{1}{s}$$ これに逆ラプラス変換をすると $$V_{OUT}=1-cos (\frac{t}{\sqrt {LC}})$$ 周波数は$\omega = \frac{1}{\sqrt {LC}}$ であるから、例えば50Hzを発振させたい場合は$\omega = 2 \pi \times 50= \frac{1}{\sqrt {LC}}$ となるようにうまくコンデンサとコイルを選ぶとする。 $L=100mH, C=100\mu F$を素子値としてプロットすると、0.2秒の間にほぼ10回振動しているのでほぼ50Hzである事がわかる。  コイルとコンデンサを組み合わせると発振する性質をうまく応用すると、直流から交流を生成できる。 例えば、コイル・コンデンサ・トランジスタを組み合わせたコルピッツ型発振回路というものがあります。 よかったら勉強してみてね。