コメント無し

# はじめに 電子回路の教科書で、必ずといっていいほど載っている回路のうちの1つに、ウィーンブリッジ発振回路というものがあります。これは正弦波 (サイン波)を発生する回路の一種であり、数十kHz程度までの低い周波数の正弦波発振に用いられる回路です。このウィーンブリッジ発振回路の発振周波数をマイコンで制御出来たら面白いのではないか、と思い立ち、制御回路を作成し実験したので、本記事で紹介したいと思います。 # 設計思想 ウィーンブリッジ発振回路の基本的な回路構成は下図のようになっています。 この回路は主に、発振周波数を決めるバンドパスフィルタと、出力振幅を制御するためのAGC回路で構成されています。 詳細な説明は、[こちら](http://www.piclist.com/images/www/hobby_elec/ckt18.htm)がわかりやすいと思います。 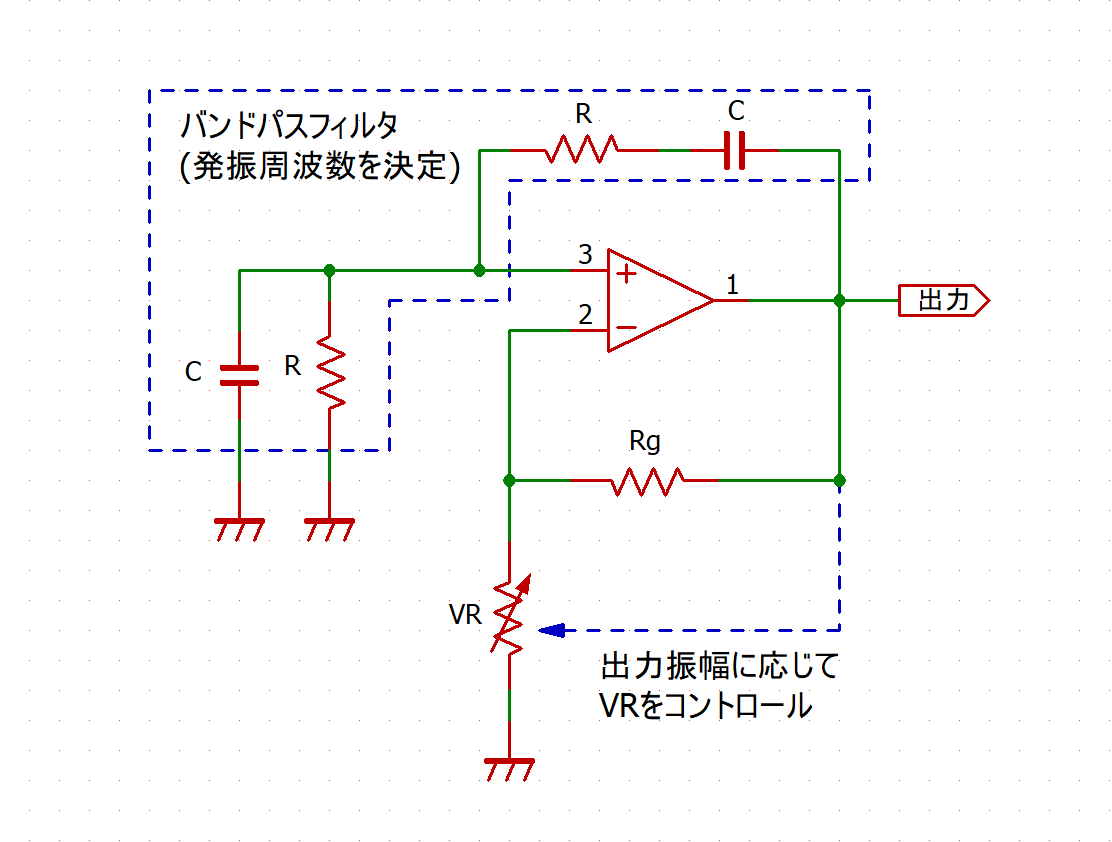 出力される正弦波の発振周波数は、バンドパスフィルタの構成によって決まり、以下の式で表されます。 $$ f = \dfrac{1}{2 \pi RC} $$ つまり、発振周波数は、$R$または$C$を変えることで変えることができます。 今回やりたいことは、こちらで指定した周波数で発振するように、マイコンによって自動的に$R$, $C$を調整する、ということです。 $R$や$C$を変える手段として、可変抵抗による抵抗値の変更や、スイッチによるコンデンサの変更などが真っ先に思い浮かびますが、これらは人間が操作することを前提に作られているため、マイコンなどで自動的に指定の周波数に合わせる、という目的には使えません。 そこで今回は、アナログマルチプレクサICである4051/4053を使って、この可変抵抗とスイッチを置き換えることを考えました。 ### 抵抗 抵抗の切り替えには、4053を使いました。4053の真理値表は以下のようになっています。 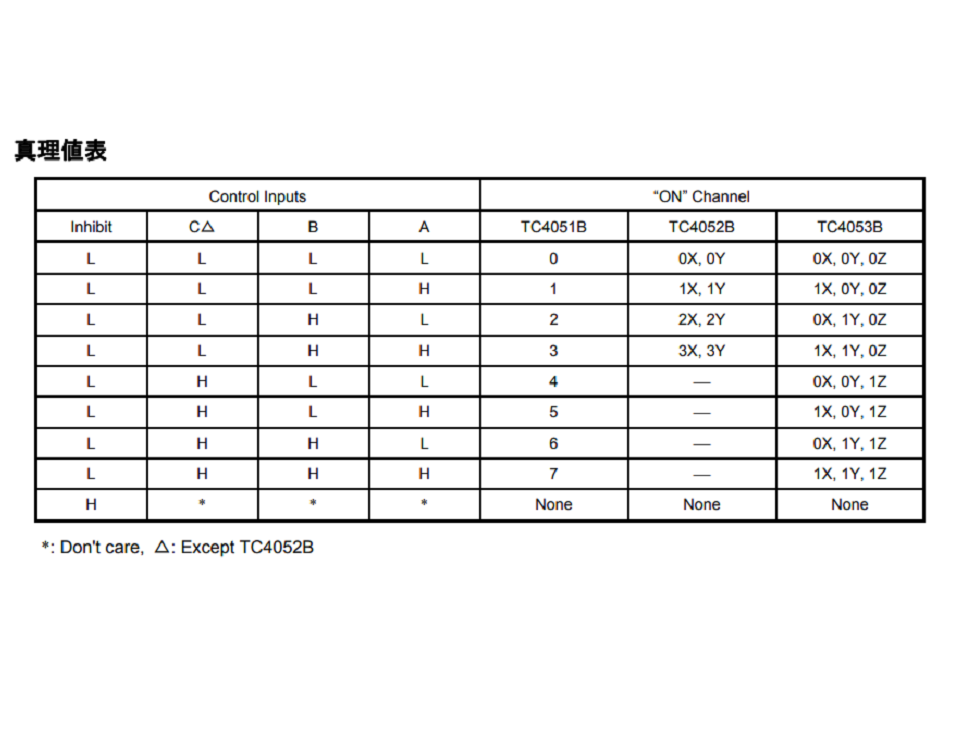 とてもざっくりとした表現をすれば、入力のH/Lにより切り替わるトグルスイッチが3個入っているようなイメージです。 下図のように4053と抵抗を配線したとき、入力がHのときには、両端の抵抗値は$R$に、Lの時には両側の抵抗値は0になります。(正確には、マルチプレクサ自体のオン抵抗が加わりますが、ここでは無視します) 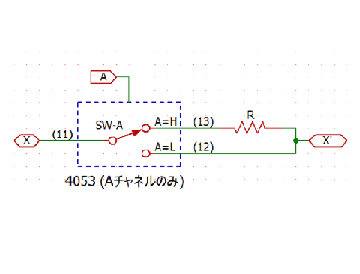 これを、抵抗値を2倍、4倍、…と増やしながら$N$個直列につないでいくと、両端の抵抗値を、$0$から$(2^N-1)R$まで、間隔$R$でデジタル的に切り替えることができます。この方法では、スイッチの数が少ないと、抵抗値はあまり変えられませんが、スイッチの数を増やすことで細かく変更できるようになります。今回はスイッチを9個、つまり、9ビット(0~511)の範囲で変えることにしました。 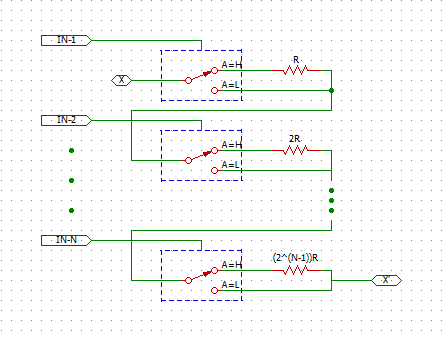 ### コンデンサ コンデンサの切り替えには、4051を使いました。 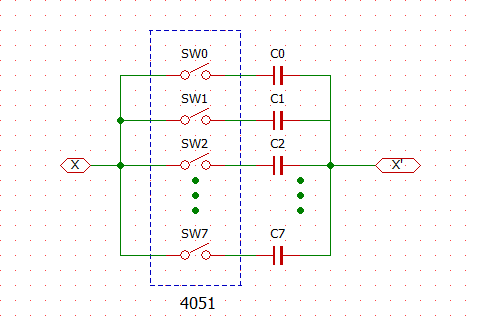 スイッチで例えると、1個のCOM端子に対し8個の端子のどれを接続するかを決める、ロータリースイッチみたいなものです。要するにスイッチをマルチプレクサに変えただけです。特に難しくないですね。 以上により、ボリュームとスイッチを、マイコンのデジタルI/Oによって操作できるマルチプレクサによって置き換えられました。 次のセクションで回路図を示しますが、ベースとなっているのはこの機構です。 # 全体の回路構成 以上を踏まえて、今回作成した回路の回路図を説明します。 今回作成した回路は、下図のようになります。 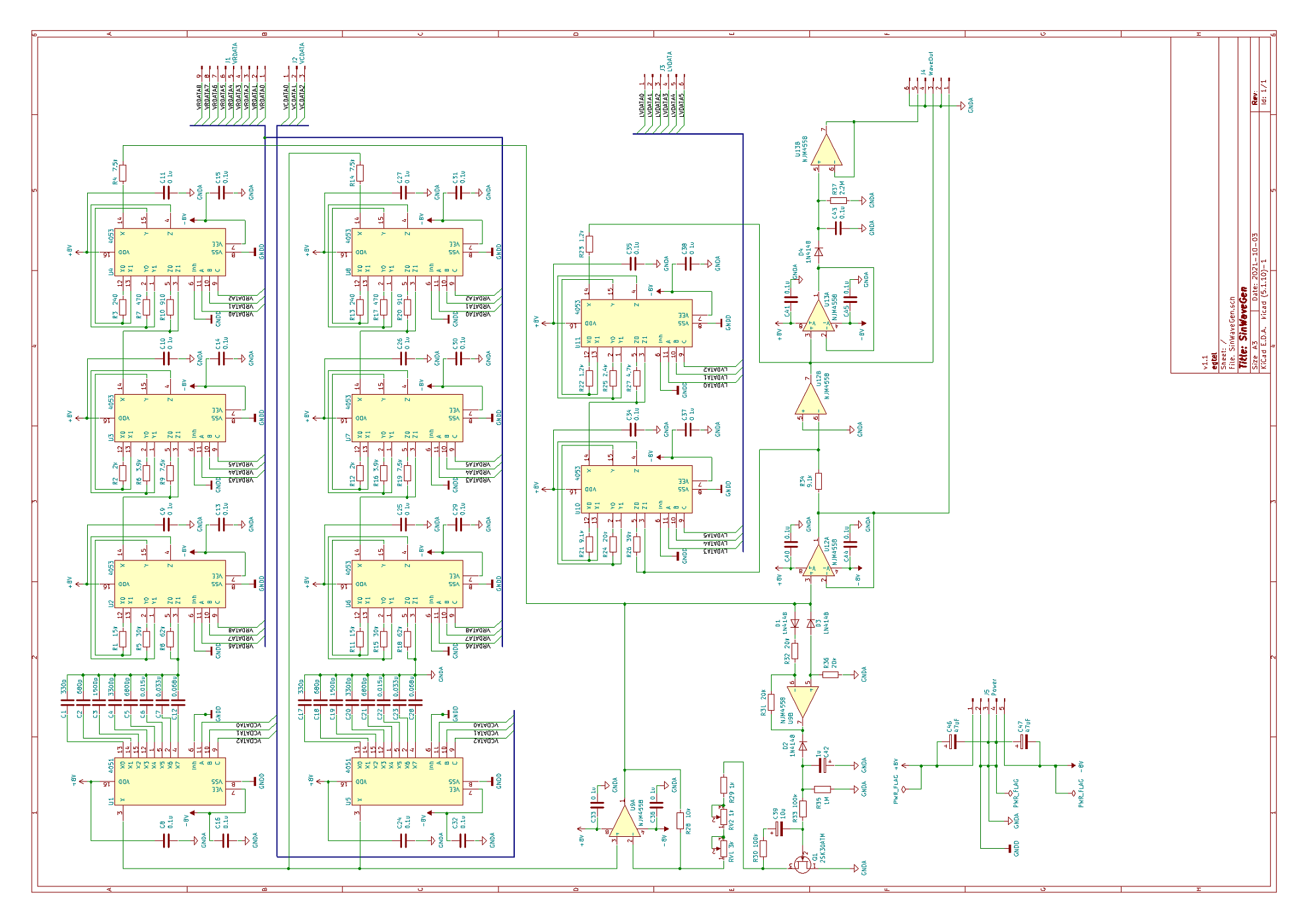 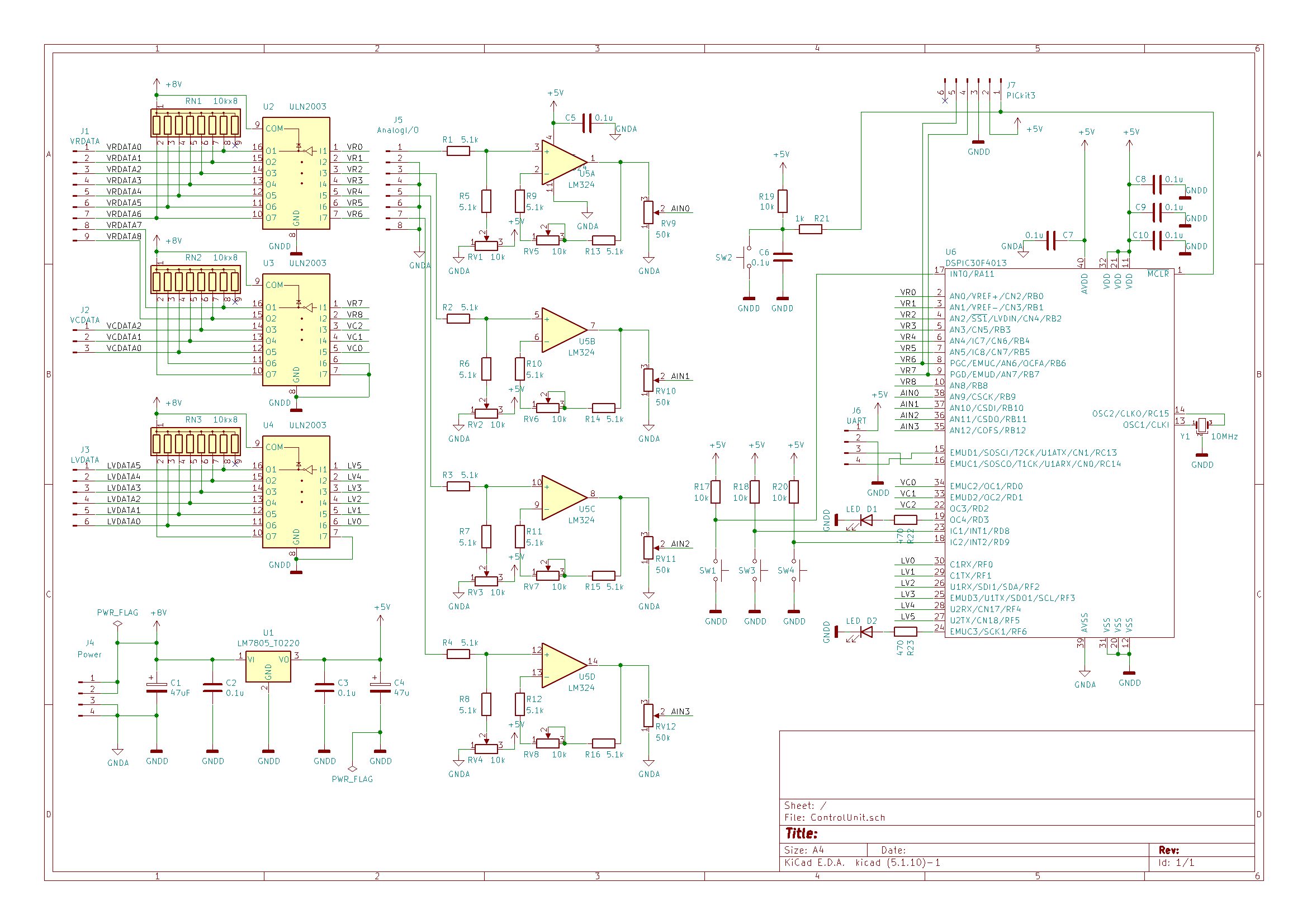 回路は主にアナログ回路部分とデジタル制御部分に分かれていて、1枚目が前者に、2枚目が後者に対応します。 ### アナログ回路部分 アナログ回路部分には、以下の機能を組み込みました。 - ウィーンブリッジ発振回路 + 発振周波数調整 (マルチプレクサ) - 出力レベル調整回路 - 出力波形のピーク値検出回路 これらは基本的に、オペアンプとマルチプレクサで構成している回路です。 ウィーンブリッジと発振周波数調整については先述の通りです。出力レベル調整回路は、オペアンプの反転増幅回路に、先述のマルチプレクサによる可変抵抗をつけてゲイン調整したものです。また、出力波形のピーク値検出回路は、ボルテージフォロワーにダイオードとコンデンサを追加し、ピーク電圧を記憶できるようにした回路です。 ### デジタル制御部分 デジタル制御部分には、以下の機能を組み込み、1個のマイコンにより制御しています。 - マルチプレクサへの出力 - 4chのアナログ入力 - USBシリアルポート マルチプレクサへの出力は、抵抗9ch + コンデンサ3ch + 出力レベル調整6chの、計18chあります。また、発振器の制御には、出力波形などの読み取りが必要になるので、4chのアナログ入力を搭載しています。また、外部インターフェースとして、USBシリアルポートを用い、TeraTermから制御・デバッグができるようにしています。 マイコンにはdsPIC30F4013を用いました。これは、必要な入出力チャンネルが、マルチプレクサ＋アナログ入力＋UARTで計24ch必要であったため、多ピンの品種である必要があったことと、当初はフーリエ変換を行うことも視野に入れており、DSPを持ち演算能力の高い品種を使いたかったことが理由になります。 (結局、DSP機能をは使用しませんでしたが) アナログ回路部分とデジタル発振部分は、別々の基板に組み込み、ジャンパワイヤで接続することで、1個のシステムとして動作させています。  # 周波数自動設定のアルゴリズム 今回作成した回路では、PCで出力したい発振周波数を指定すると、dsPICによって、実際にその周波数を出力するように抵抗・コンデンサを自動で調整できます。見づらいですが、下のツイートの添付動画のように、TeraTerm上で周波数を設定できます。 @[twitter](https://twitter.com/electrotelecast/status/1463451403364417540?s=20) ここでは、この自動設定のアルゴリズムと、そのテスト結果について軽く紹介します。 ### やっていること 大まかな流れとしては、上記の1~4の手順で行います。 1. 指定された発振周波数から、抵抗値・容量値を仮決定する。 1. 仮決定した抵抗値・容量値における発振周波数を測定する。 1. 測定した発振周波数と、目標の周波数との誤差を求める。誤差が指定した値以下なら、設定完了とする。 1. 誤差が大きい場合は、求めた誤差から抵抗値の補正値を決め、抵抗値を再設定し、2に戻る。

2については、発振波形をマイコンのADCによってモニタし、振幅中心を波形が通過する回数と、その回数通過するのにかかった時間から、1秒当たりの通過数、つまり、発振周波数を求めます。 3については、目標周波数の相対誤差 $Error$を、以下のように定義して計算しています。 $$ Error=\dfrac{\Delta f}{f} = \dfrac {f_{measure}-f}{f} $$ ただし、$f$ は目標の周波数を、$f_{measure}$は2で測定した周波数を表します。この誤差が、指定した数値を下回ると、周波数の設定は完了したものとみなします。 4については、補正値を。周波数の式$f=1/(2\pi RC)$をテーラー展開することで近似的に求めました。 その過程を以下に示しますが、苦手な方は読み飛ばしていただいて構いません。

$$ f+\Delta f = \frac{1}{2\pi (R+\Delta R)C} $$ この式を、テーラー展開を用いて変形していくと、 $$ f+\Delta f = \frac{1}{2\pi RC}\frac{1}{ 1+ \frac{\Delta R }{R}} = f\frac{1}{ 1+ \frac{\Delta R }{R}}$$ $$ = f \Big(1-\frac{\Delta R}{R}+\Big(\dfrac{\Delta R}{R}\Big)^2-\cdots \Big) $$ $$ \approx f-f\frac{\Delta R}{R} $$ となります。この式をまとめて整理することで、抵抗値のズレ$\Delta R$は、 $$ \Delta R =-R \frac{\Delta f}{f} =-R\times Error$$ と表されます。ここで、$\Delta R$が$R$に対して非常に小さいと考え、現在の抵抗値 を$R_{present}=R+\Delta R\approx R$とみなすと、$\Delta R$を0にするための抵抗の補正値$R_{correct}$は、 $$ R_{correct} = R_{present}\frac{\Delta f}{f}=R_{present}\times Error $$ となります。これを補正値として、2に戻るときの抵抗値を、$R_{next} = R_{present} + R_{correct}$として再設定します。 以上のようにして、1~4の手順を繰り返していくことで、目標の周波数を求めることができます。 ### 周波数自動設定のテスト結果 上記アルゴリズムの有効性を調べるために、以下の10種類の周波数を自動設定してみました。 1列目に記載した目標周波数に対して、発振周波数の誤差が±1%以内に収まるように自動設定させた後の周波数を2列目に記載しています。また、3列目は、目標周波数に対する実際の周波数の誤差を表し、4列目は3列目の誤差が±1%以内に収まっていれば〇を、収まっていなければ×を記載しています。 | 目標周波数(Hz) | 自動設定後(Hz) | 誤差(%) | 判定 | |:---:|:---:|:---:|:---:| |20|20.02|0.100|〇| |100|99.206|-0.794|〇| |500|503.01|0.602|〇| |1k|999.001|-0.100|〇| |2k|1.998k|-0.100|〇| |2.5k|2.505k|0.200|〇| |5k|5.020k|0.400|〇| |7.5k|7.389k|-1.480|×| |10k|10.101k|1.010|×| |20k|10.593k|-47.035|×| 上表から、目標周波数が5kHz以下であれば、上記アルゴリズムによって自動的に周波数を設定できていることがわかります。しかし、それより大きい周波数になると、目標周波数の±1%以内に収めることができていません。 この原因として考えられるのは、以下の3点です。 - そもそもアルゴリズムに間違い/不備がある。 - dsPICのADCサンプリング速度が不足しており、正確な周波数計算ができていない。 - ウィーンブリッジ発振回路のゲイン調整回路が高周波に対応していない。 特に3番目は、自動設定中に安定した発振が維持できていないことが、オシロ波形から確認しており、より高周波の正弦波を作るには発振回路そのものの設計を見直す必要があると考えられます。 ### 出力波形 テスト時に取得した発振波形を以下に示します。(ただし、写真のキャプションは設定周波数を表す) 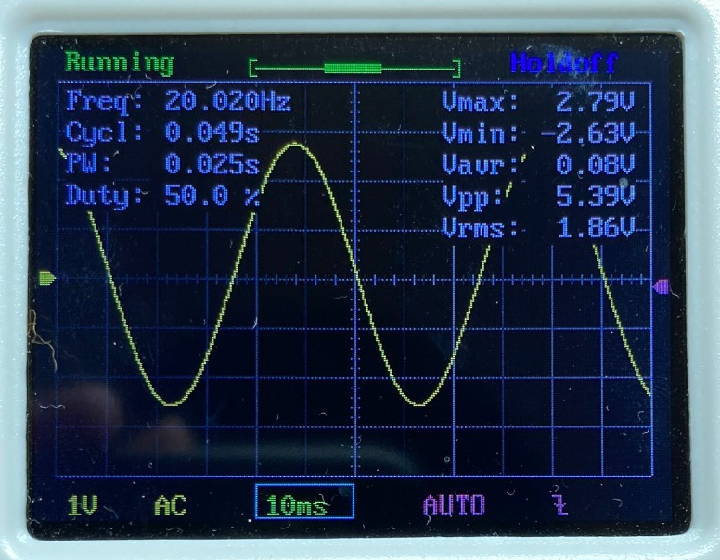 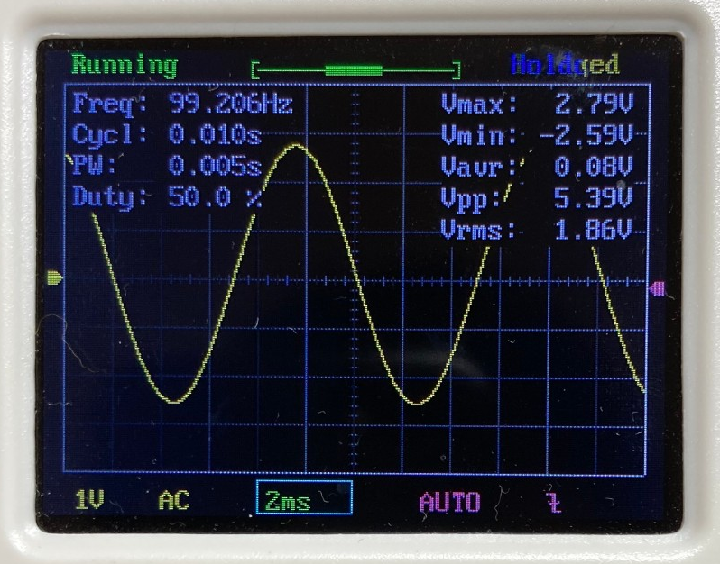 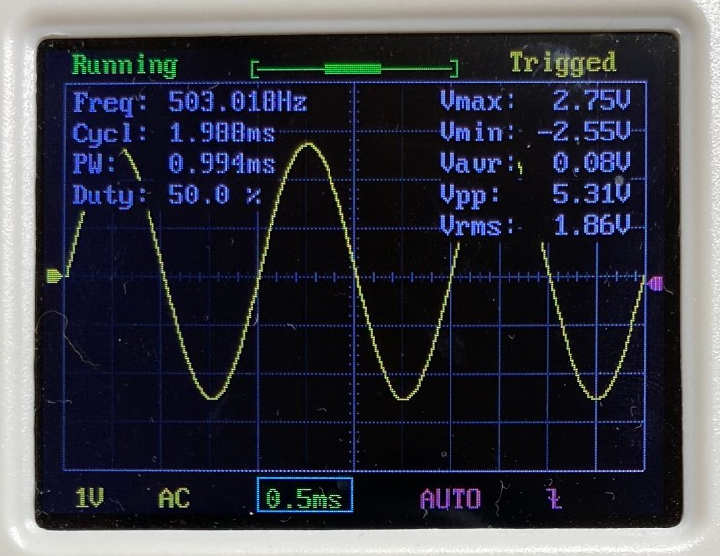 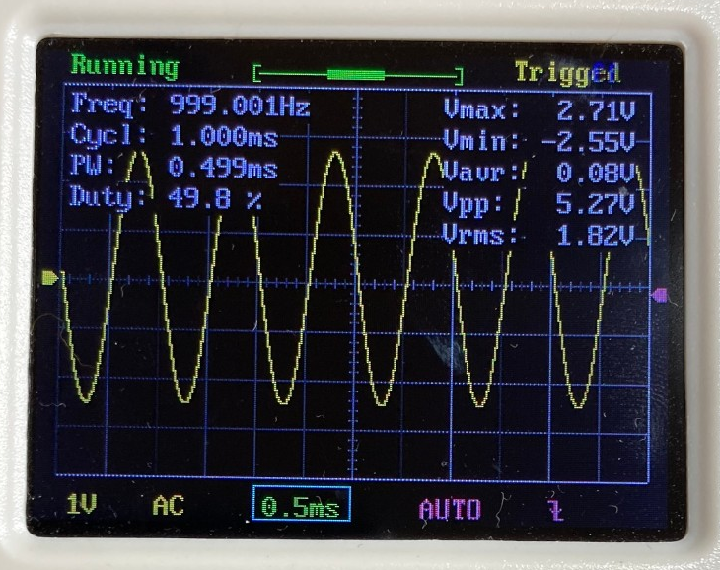 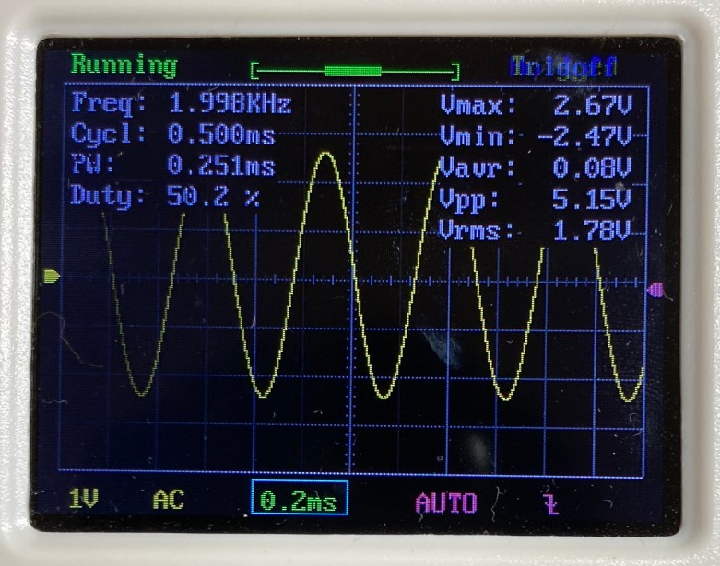 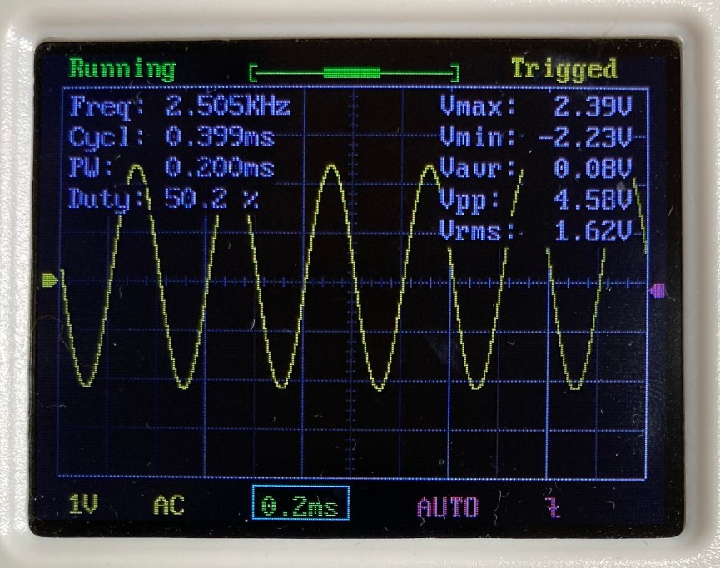 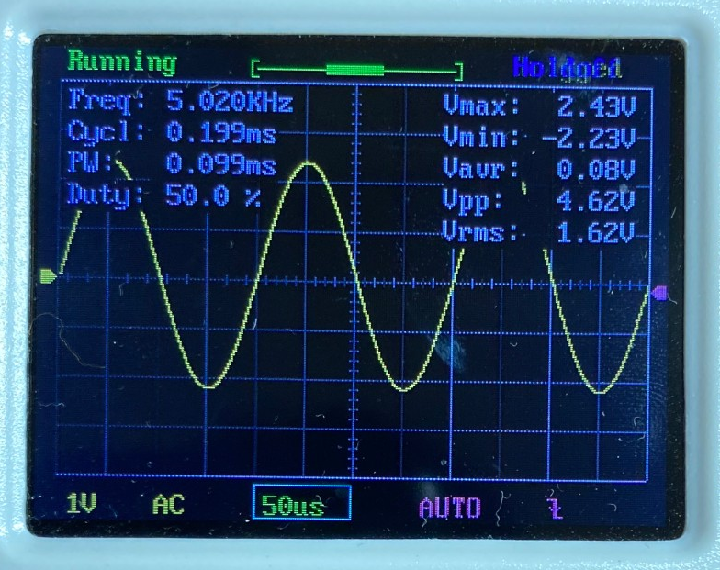 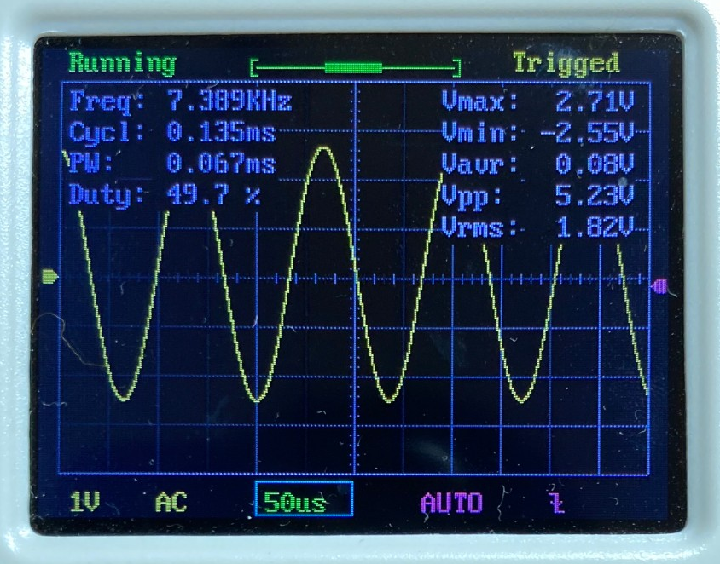 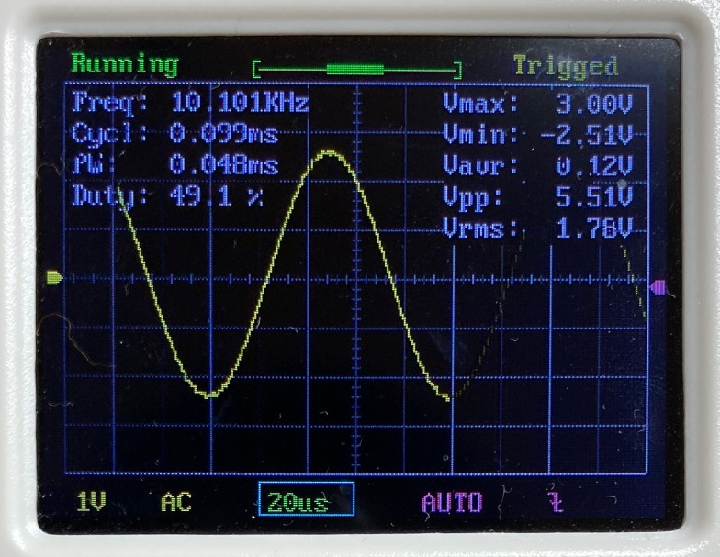 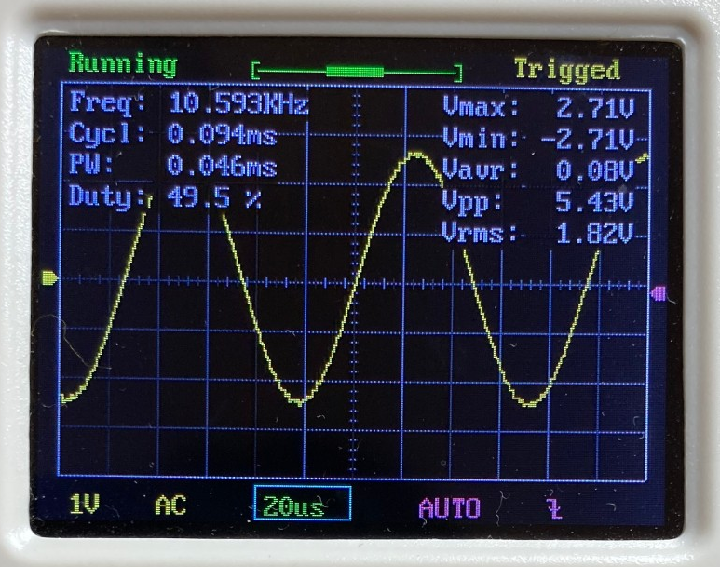 # まとめと課題 今回作成した回路で達成できたことと今後の課題は以下の通りです。 今後の課題については、アナログ回路部分の設計から見直す必要がありそうなので、再度時間やる気が確保できたら取り組みたいです。 ==達成できたこと こちらで指定した周波数を出力するように、ウィーンブリッジ回路の抵抗・コンデンサをdsPICマイコンで自動調整すること== ++今後の課題 ・5kHzより高い周波数を設定できないこと ・搭載した出力レベル調整回路とピーク値検出回路を活用できていないこと++