初版

MSGEQ7の応用可能性を探ってみた

セットアップや使用方法

(CC BY-NC-SA 4+) Creative Commons Attribution-NonCommercial-ShareAlike CC BY-NC-SA version 4.0 or later

# はじめに Mix Signal Integration社が発売しているMSGEQ7は、数個の外付け部品による簡単な回路構成で動作するスペクトルアナライザICである。その手軽さから、ネットでもオーディオ用のスペアナの製作記事を複数見つけることができる。 本記事では、そのようなICの外付け部品を少し変更することによる(若干の)応用可能性を見出したので備忘録を兼ねてまとめる。 # MSGEQ7の概要 MSGEQ7は入力信号のスペクトルを7バンドに分割し、それぞれの周波数領域における周波数成分を出力することができる。出力される周波数成分は下図のように、入力信号に63Hz, 160Hz, 400Hz, 1kHz, 2.5kHz, 6.25kHz, 16kHzの成分が含まれるとき、それぞれの周波数に対応する出力電圧が高くなり、出力電圧の高低により、入力電圧のスペクトル、つまり、入力に含まれる周波数成分の高低を知ることができる。 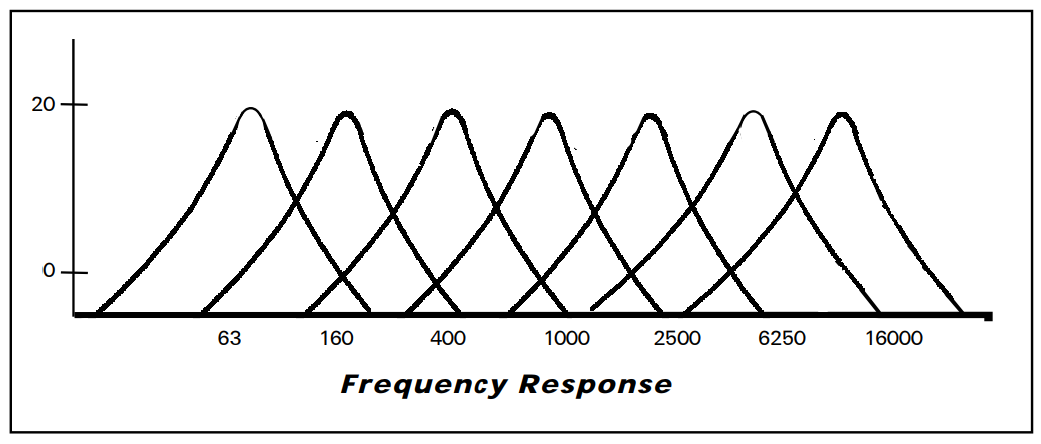 実際のICの出力は、制御信号であるSTROBEとRESETによって、OUT端子に出力する周波数成分の周波数を切り替えることで行う(下図)。例えば、Ardiuno等のマイコンに接続して使用する場合、マイコンの出力ポートでSTROBE信号を発生させながらOUT端子の電圧を読み取っていくことで、連続的にスペクトルを読み込むことができる。 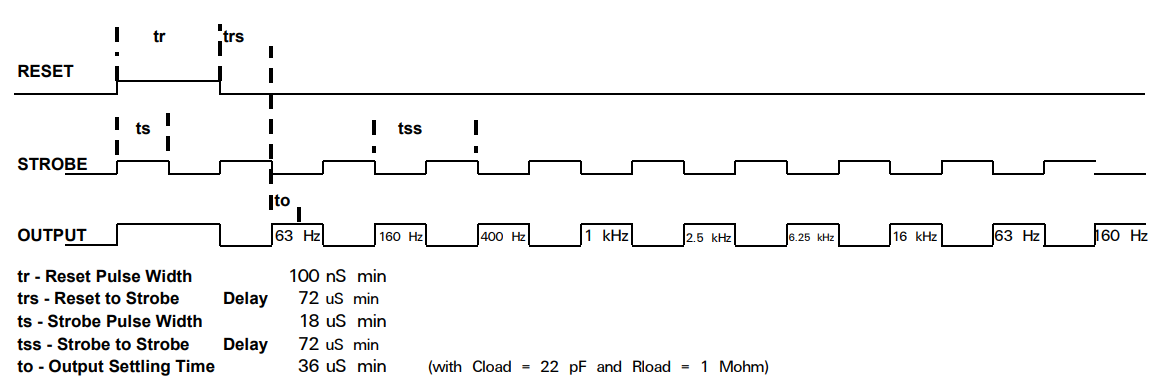 より詳細な動作や諸特性等は、メーカーが公開している[データシート](https://mix-sig.com/images/datasheets/MSGEQ7.pdf)を参照していただきたい。 # 推奨回路での動作 まずは、データシートの「Typical Application」に掲載されている回路ベースに実験用回路を作成し、動作テストを行った。回路はほぼデータシート通りであるが、入力信号(IN)の入力はDigital Discoveryで矩形波を入力して行ったため、カップリングコンデンサの前段に信号レベル調整用の可変抵抗を入れた。 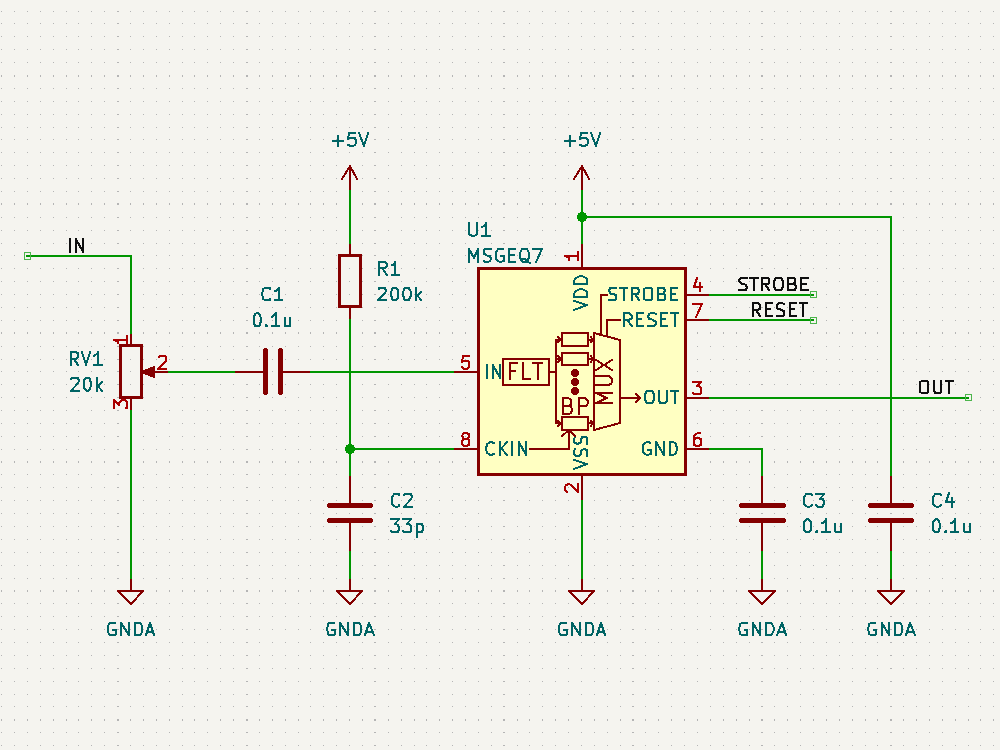 STROBE、および、RESETはDigital Discoveryに接続し、下図のような制御信号を送った。これにより、2入力のオシロスコープを用いて、RESET信号でトリガをかけてOUT端子を見ることで、各ピークの高さを安定的に測定できるようにした。  上記の条件で、入力端子にVp-p=約184mVの矩形波を、周波数を変えて入力することで以下のような波形が得られた。矩形波は、発振周波数を一番下の基本周波数と、基本周波数の2倍、4倍、6倍…の周波数成分が減衰しながら合成してできている波であるので、矩形波の中心周波数をピークの中心周波数に合わせることで、対応するピークが高く表れていることが確認できる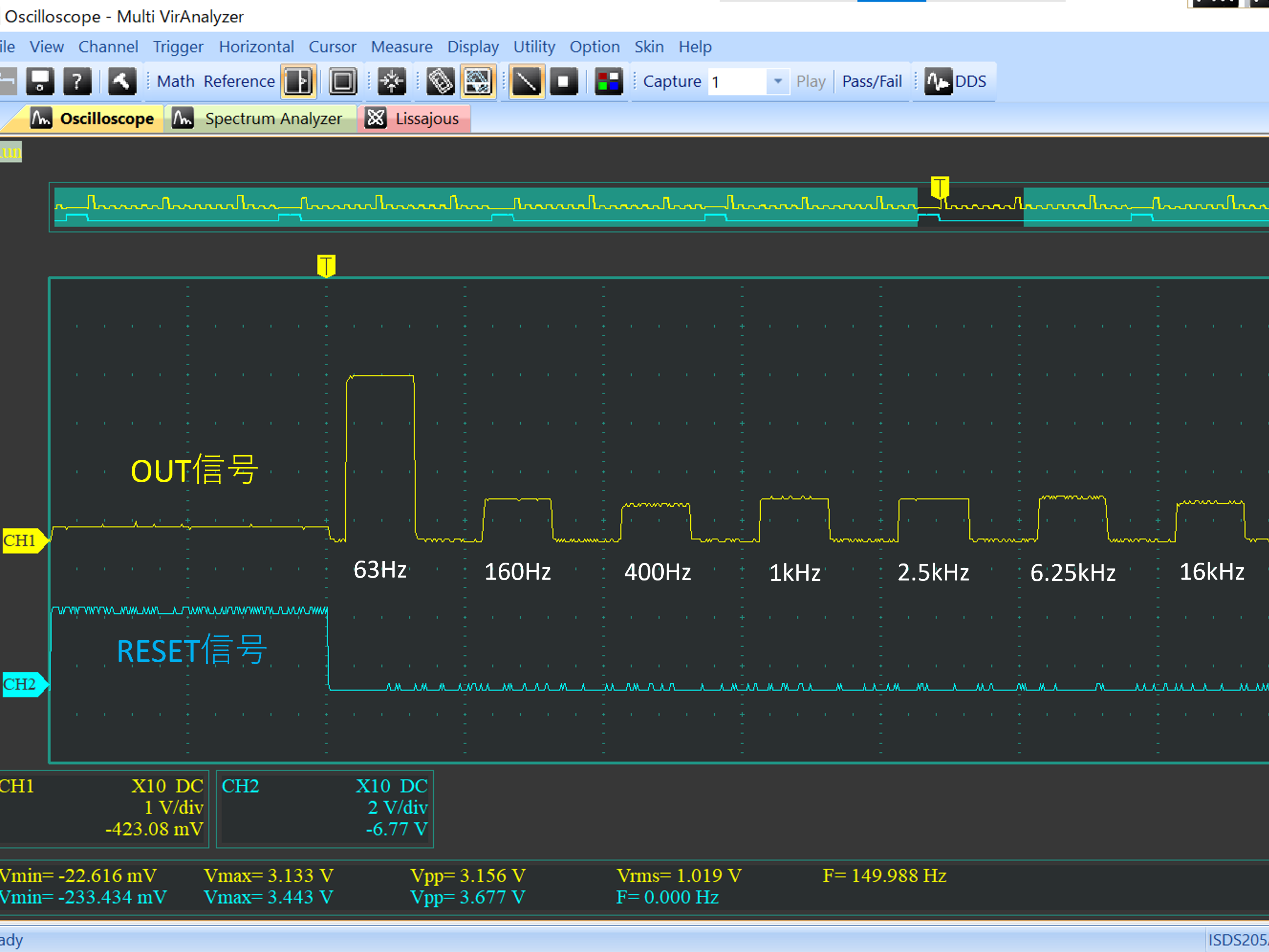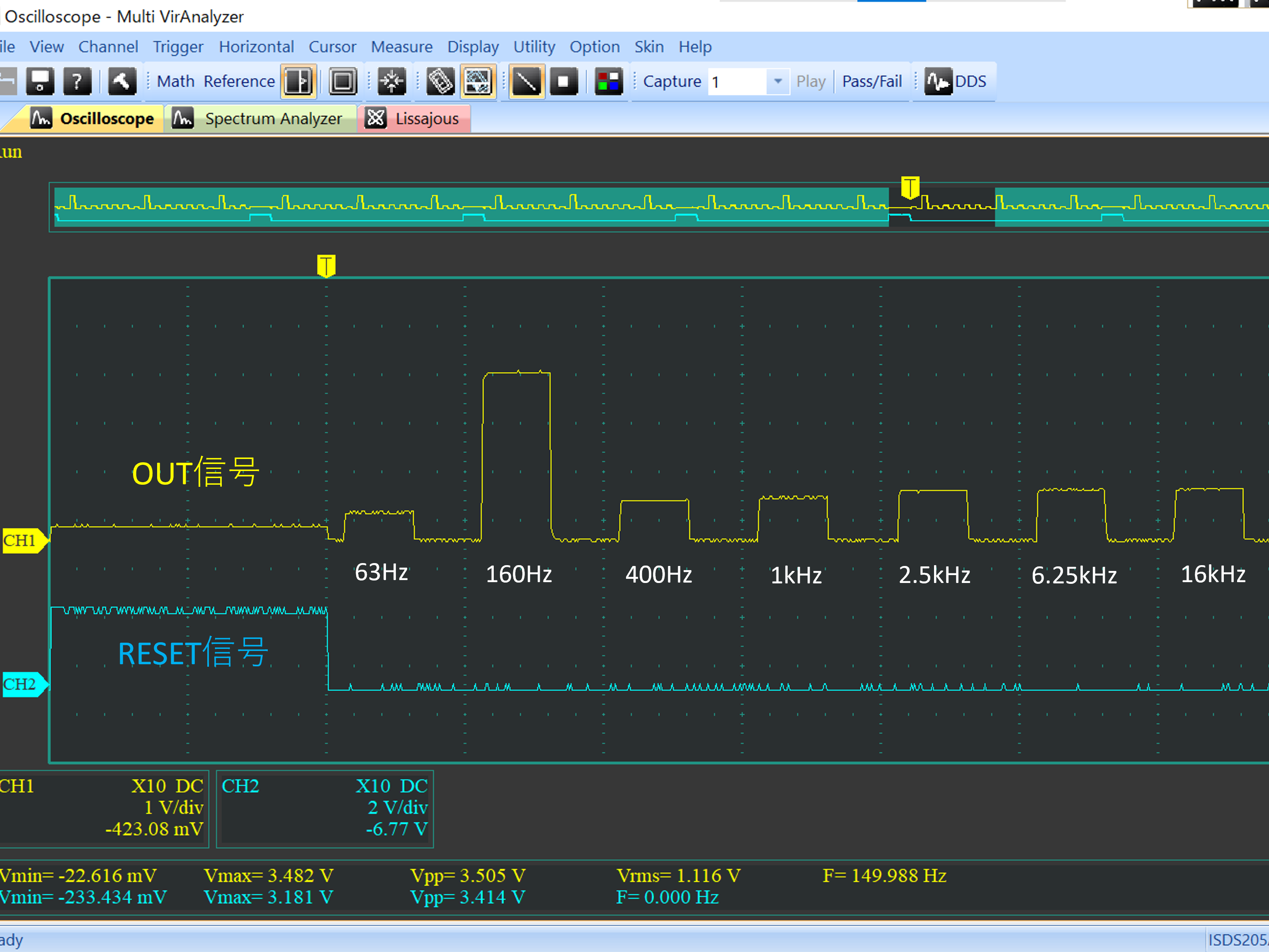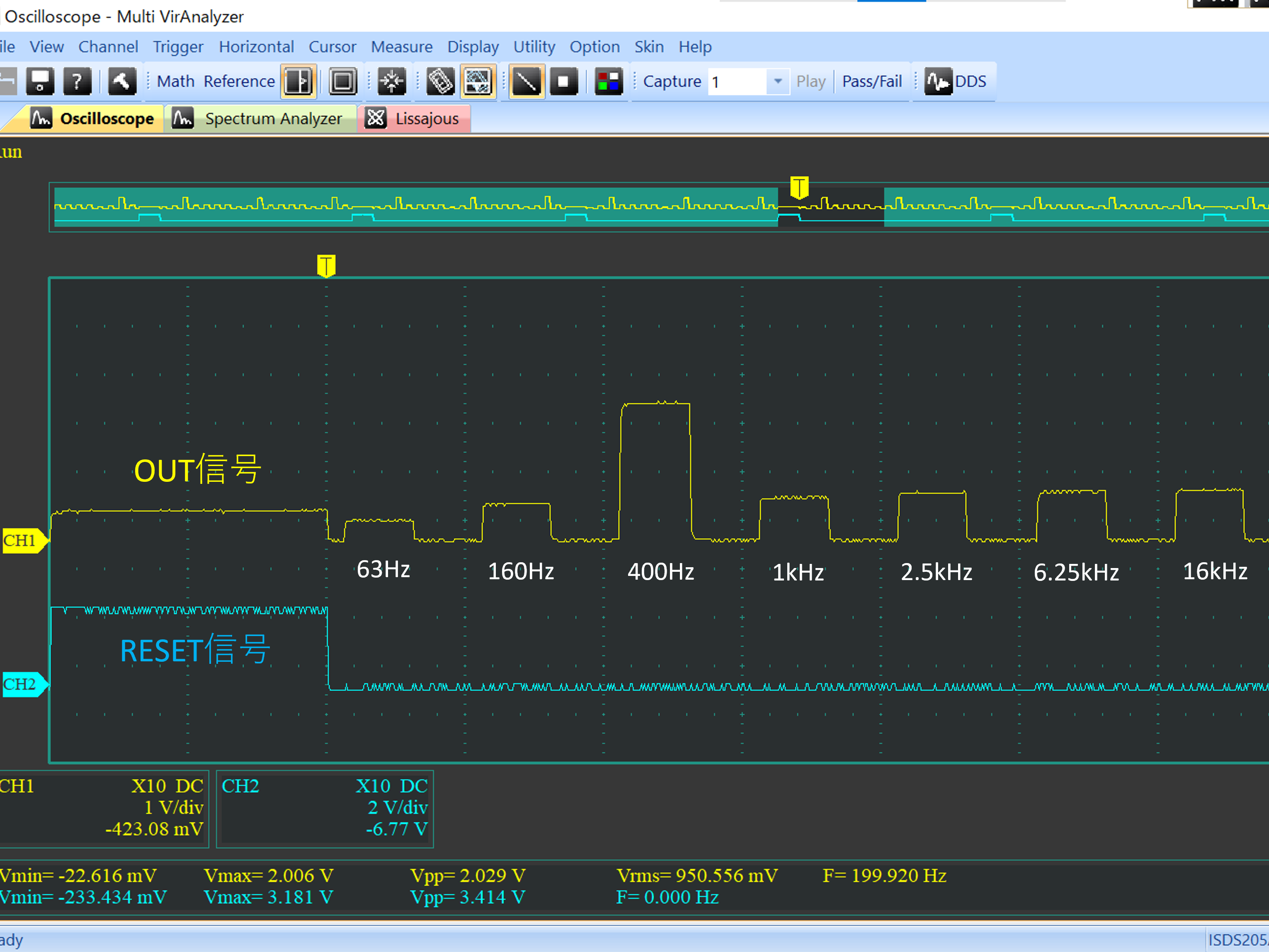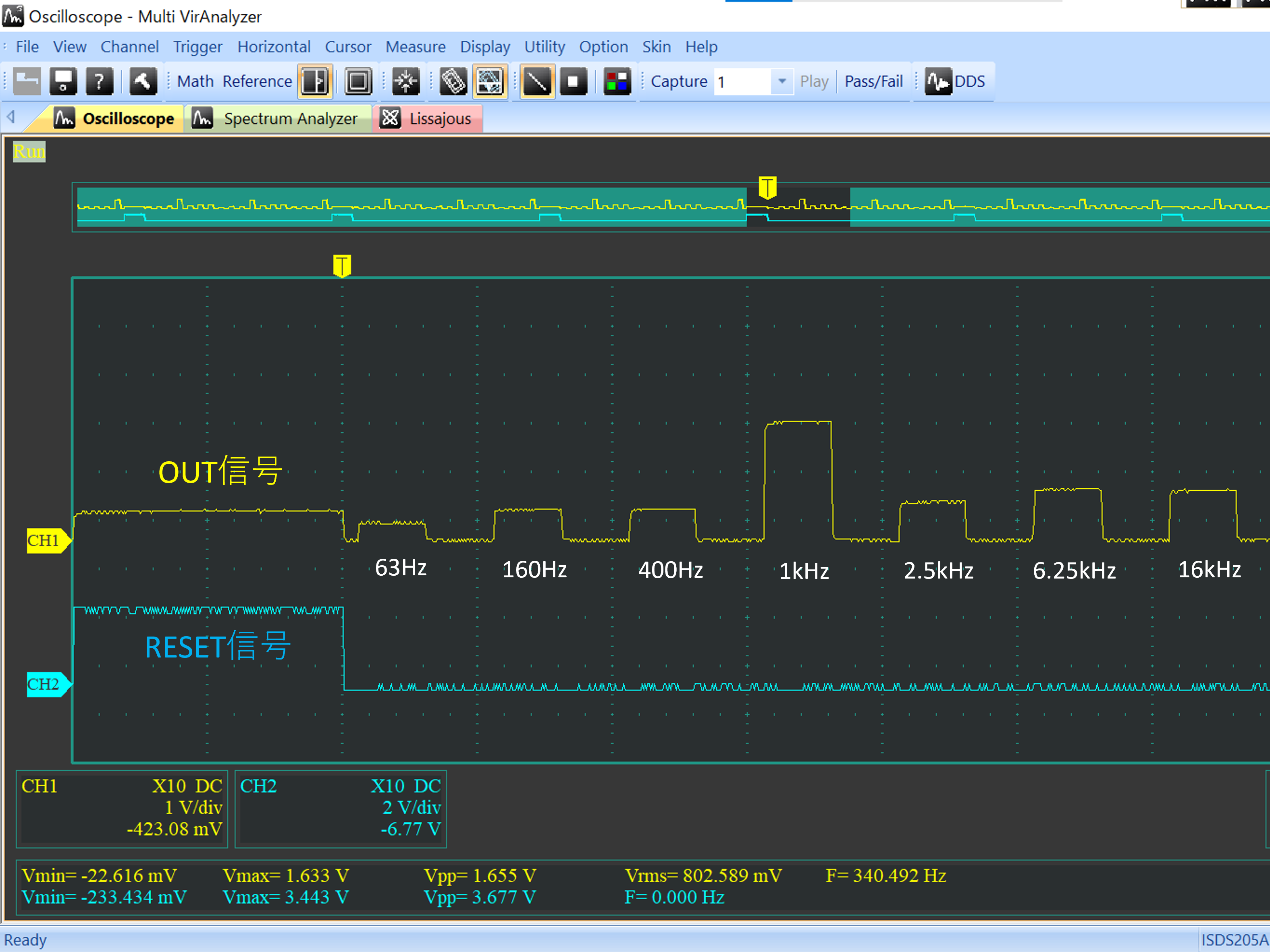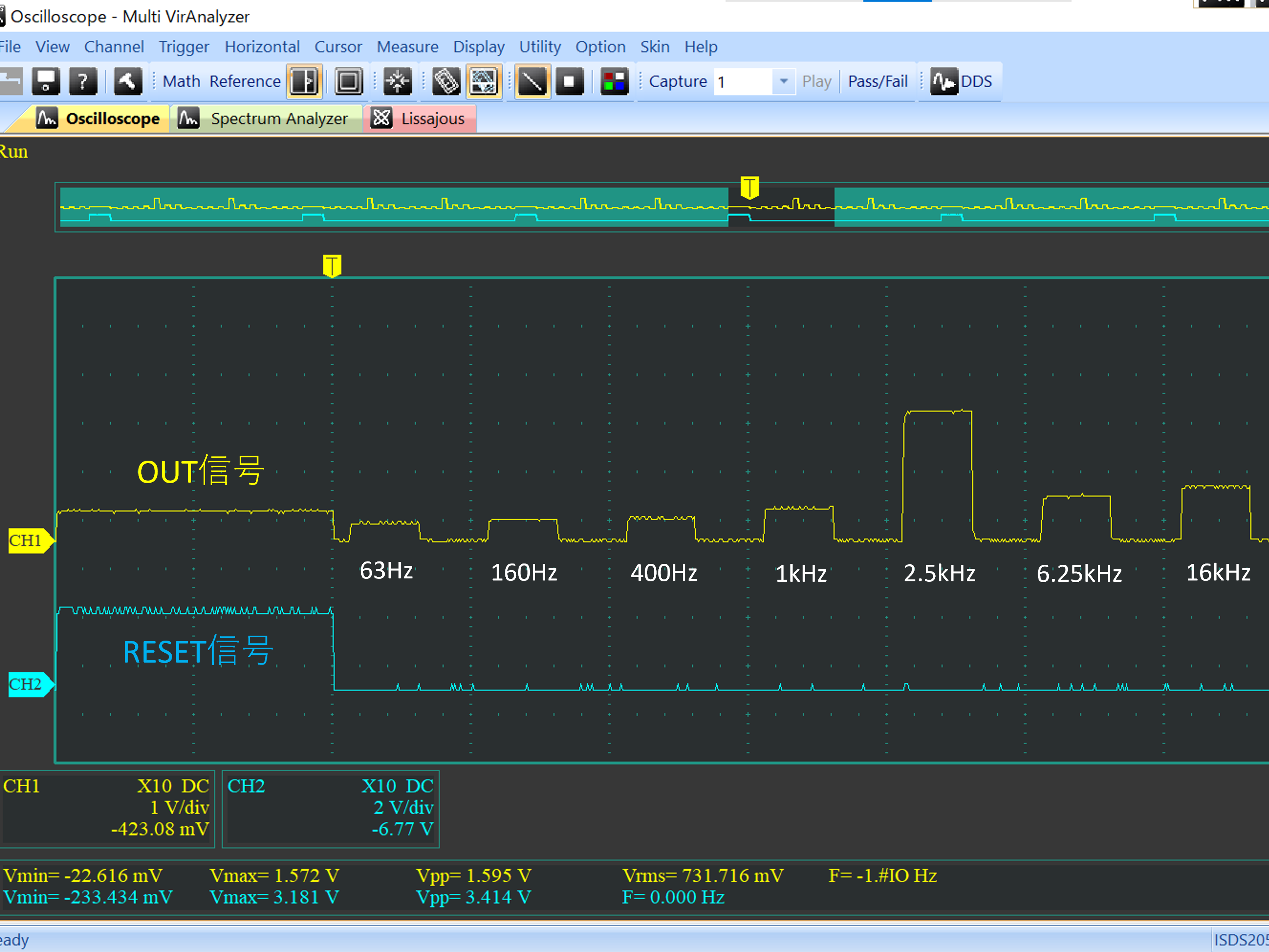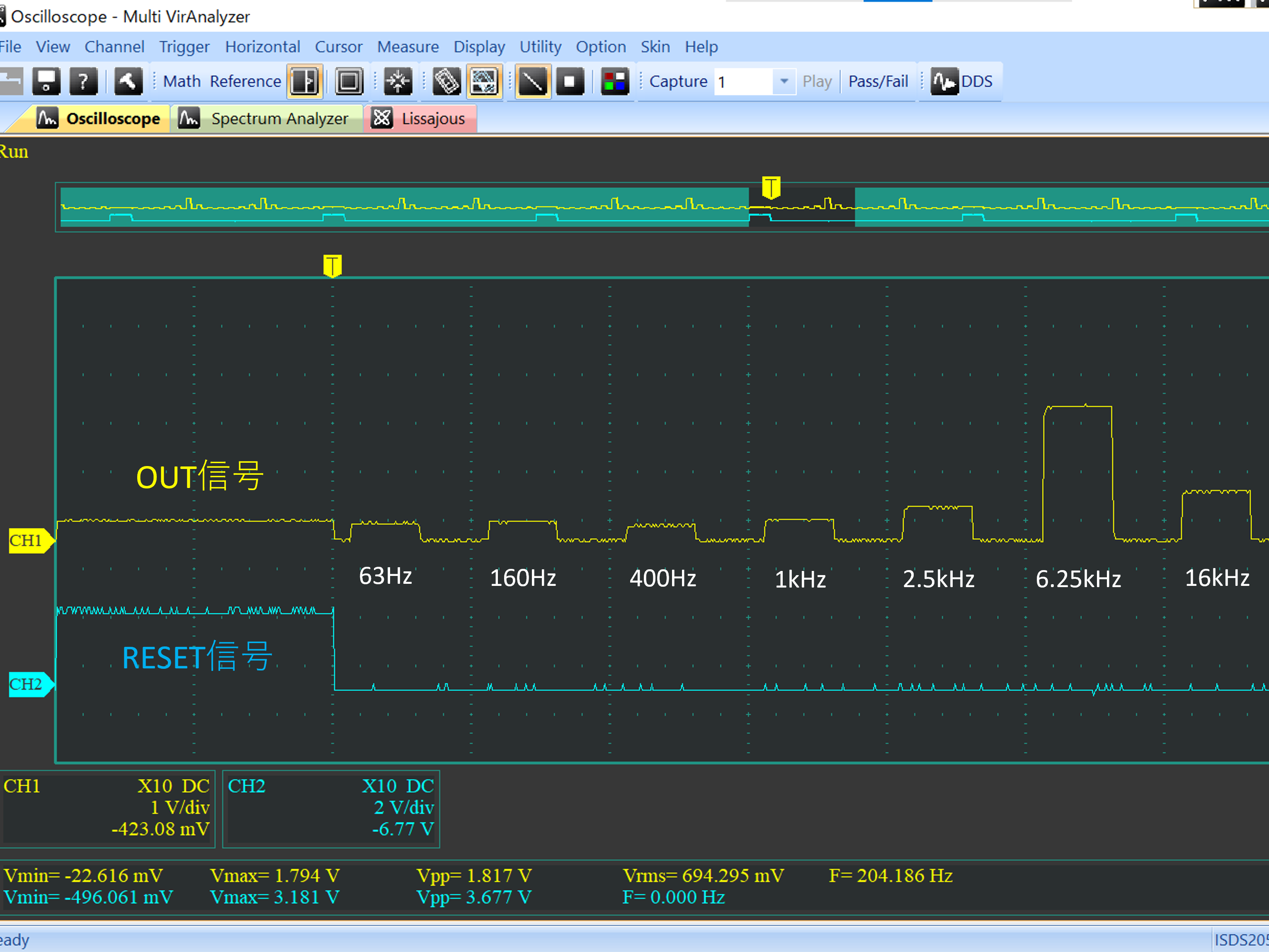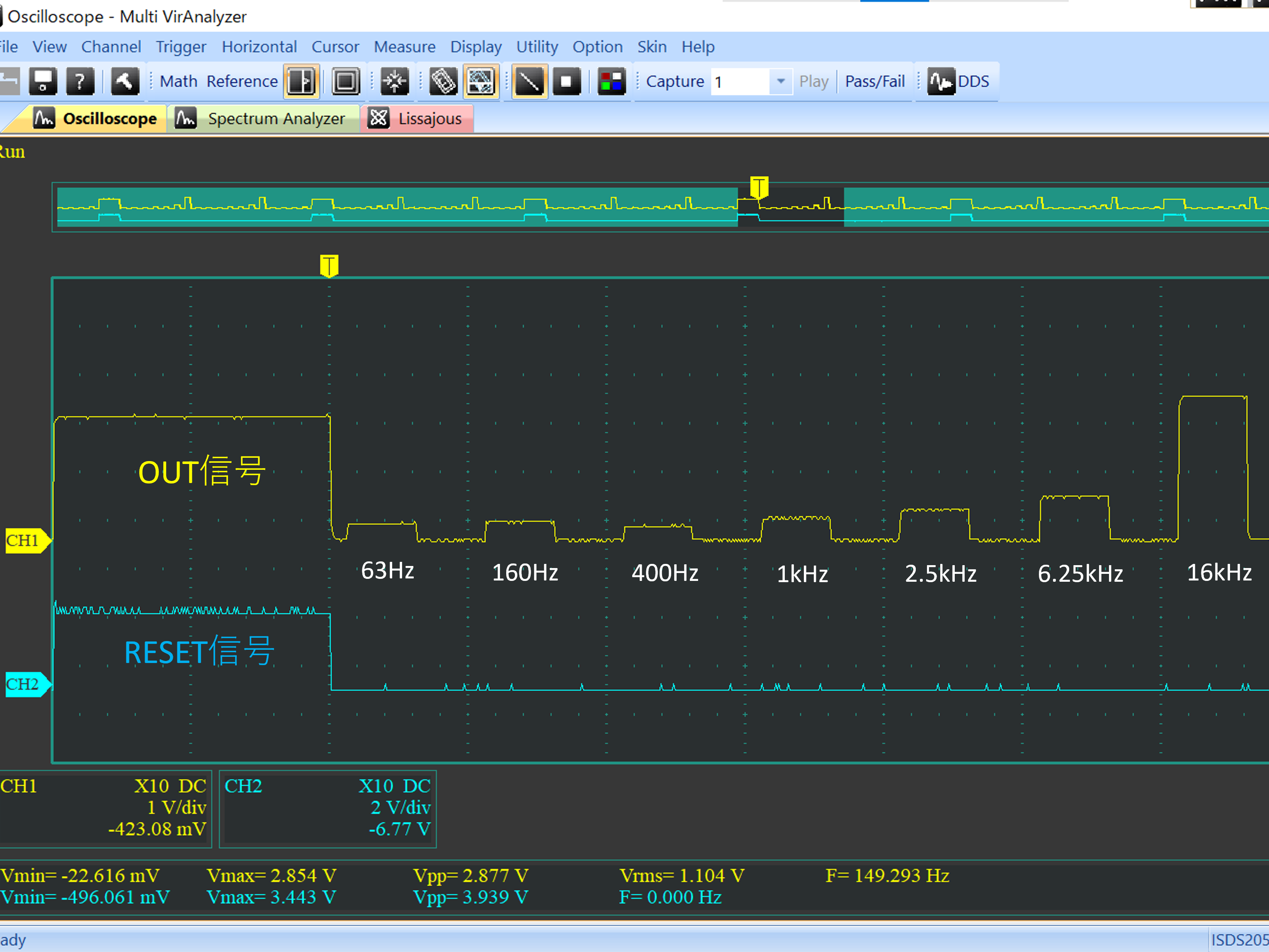。 |  |  | |:---:|:---:| |  |  | |  |  | |  | | 以上から、推奨回路での正常動作を確認することができた。 # CKINに接続する抵抗を変更してみる 次に、推奨回路のCKIN (8pin)に接続する200k$\Omega$から別の抵抗値に変更したとき、出力波形がどのように変化するかを確認した。抵抗値の変化は以下の2パターンを試した。 1. 200k$\Omega$から500k$\Omega$に変更し、周波数400Hz, 1kHzの矩形波を入力する。 1. 200k$\Omega$から400k$\Omega$に変更し、周波数200Hz, 500Hzを矩形波を入力する。 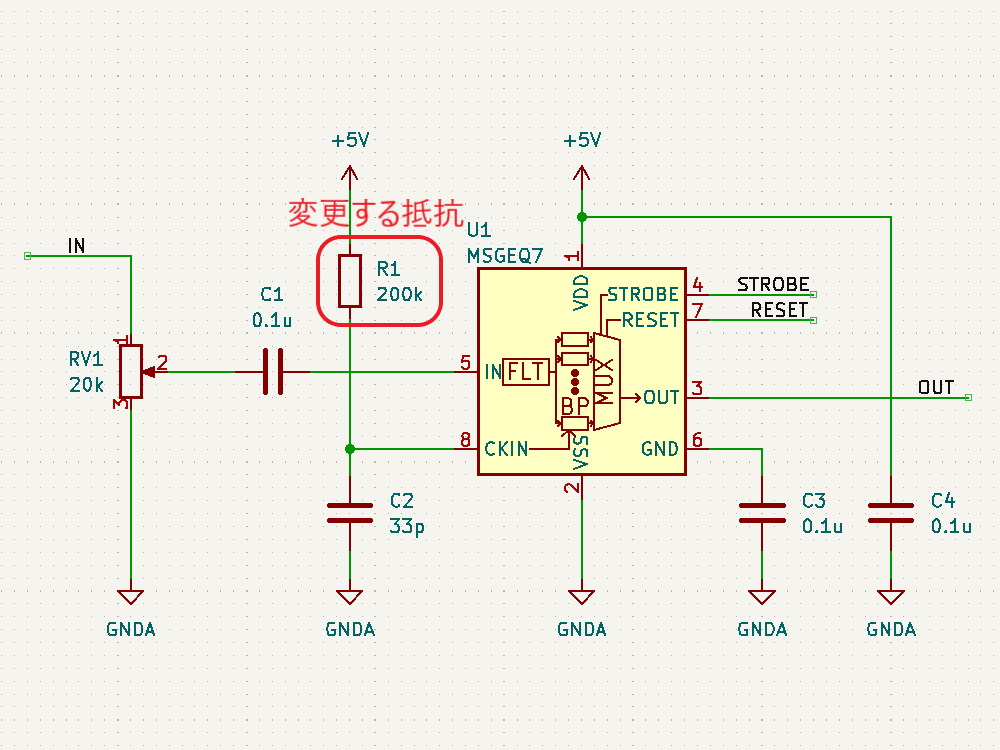 ## 1の場合 抵抗値が推奨回路通りの200k$\Omega$の時、各入力周波数におけるピークが立っている状態である。 この抵抗値を200k$\Omega$から500k$\Omega$に変更すると、200k$\Omega$の時の1個上の周波数にピークがシフトする。つまり、CKINに接続する抵抗値を、推奨回路の2.5倍に変更することで、回路内部の見かけの周波数が2.5倍となり、入力周波数を変えなくても2.5倍の周波数で表示されていることが推測される。 | 入力周波数 | 200k$\Omega$ (規定) | 500k$\Omega$ (変更) | |:---:|:---:|:---:| | 400Hz | 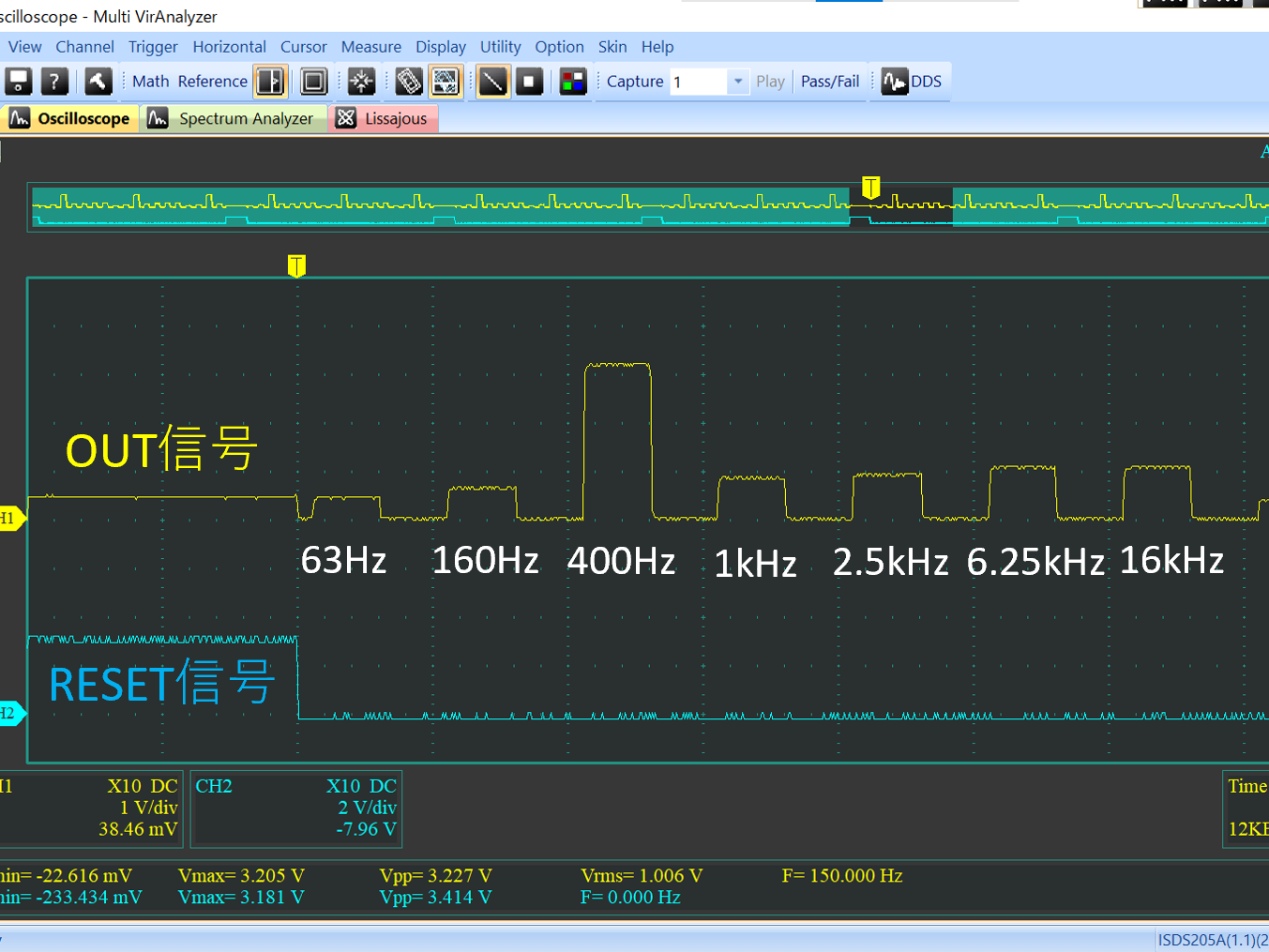 | 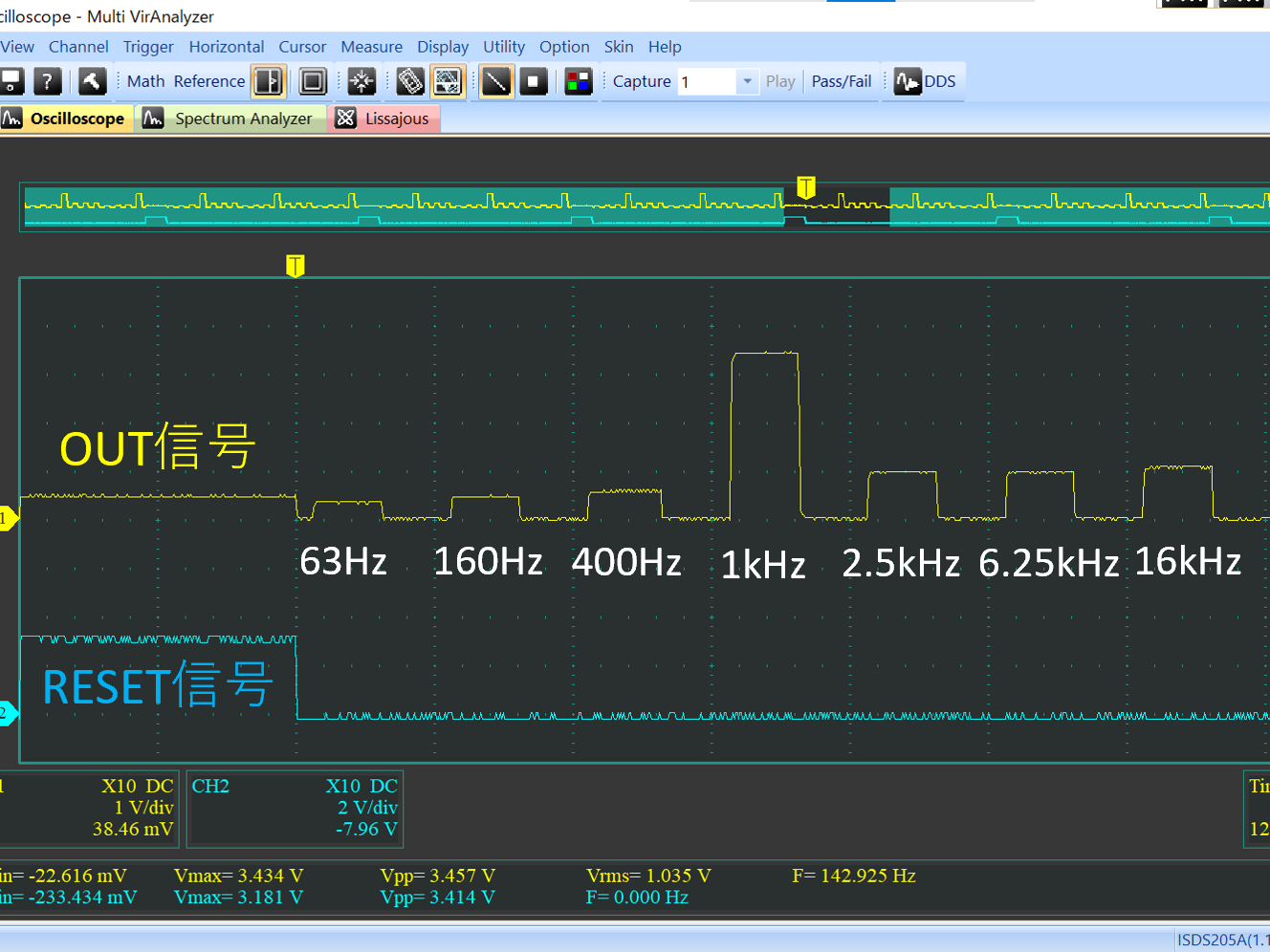 | | 1kHz | 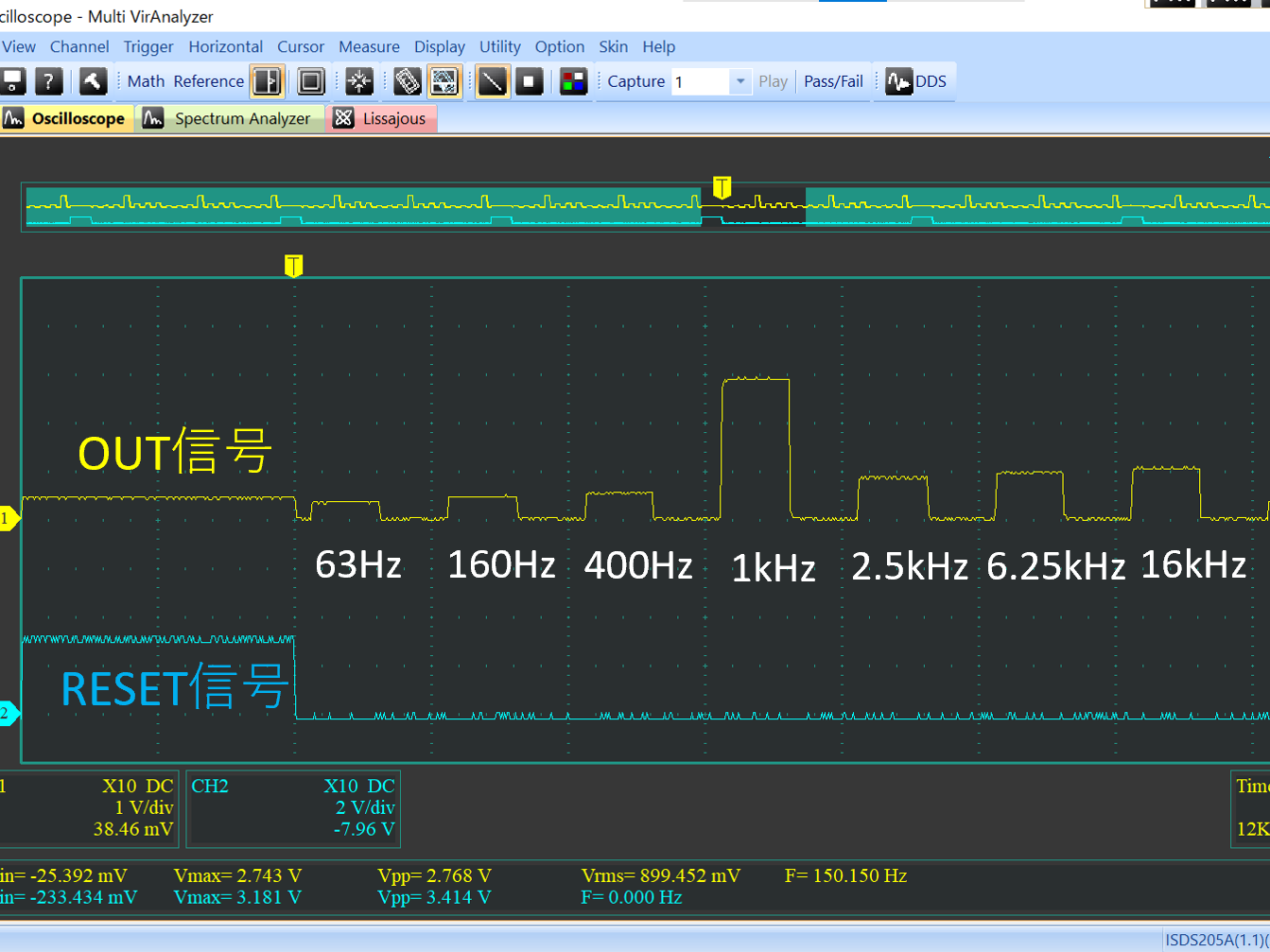 | 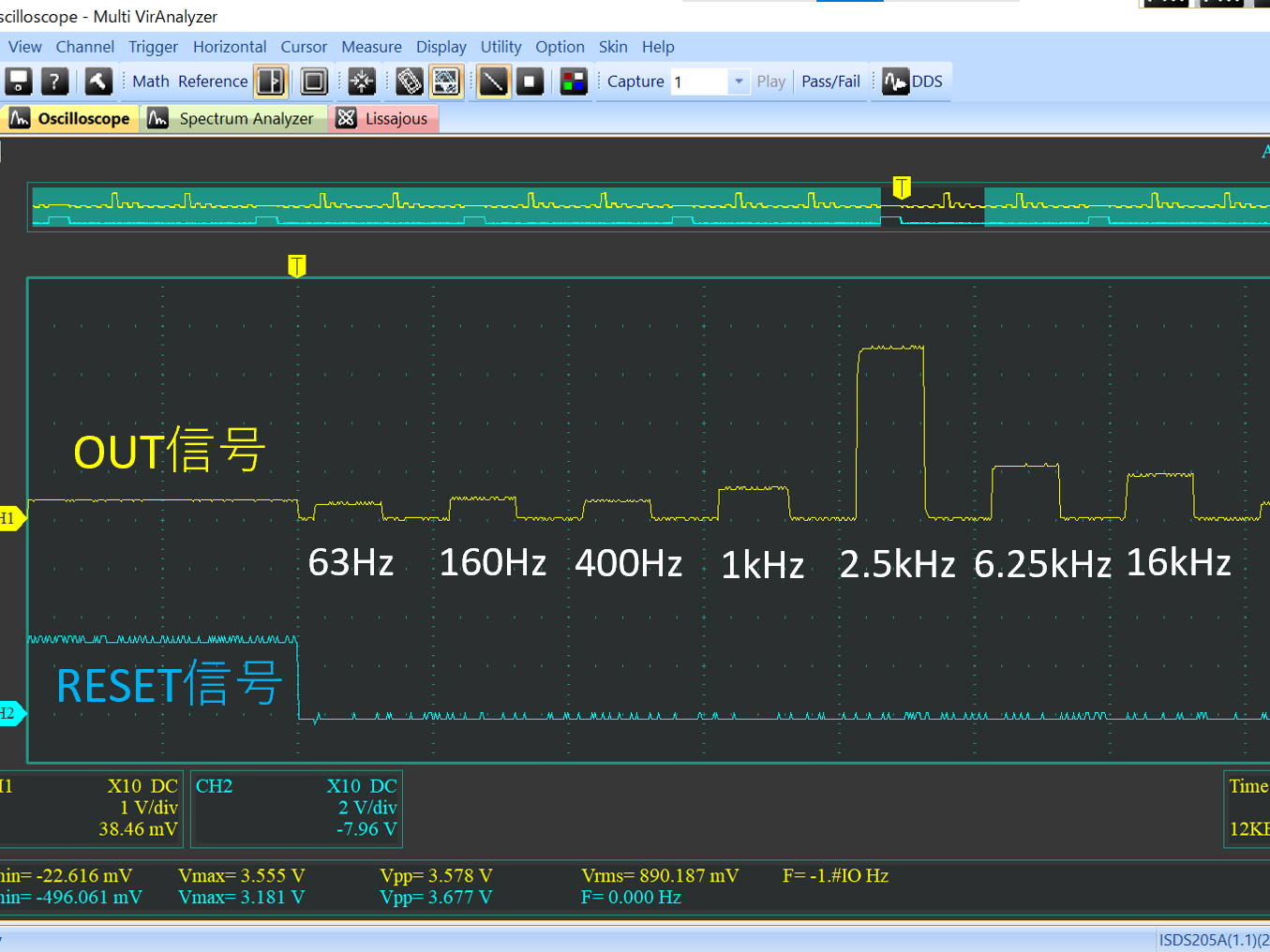 | ## 2の場合 抵抗値が推奨回路通りの200k$\Omega$の時、各入力周波数では特定の周波数でピークが立っていない状態である。これは、入力周波数が、どちらも推奨回路におけるピークの中心周波数の半分であることから説明がつく。 この抵抗値を200k$\Omega$から400k$\Omega$に変更すると、入力周波数の2倍の周波数にある、ピークの中心周波数で出力のピークが立った波形が得られた。これは、1と同様、抵抗値が2倍になったことで回路内部の見かけの周波数が2倍となり、出力としては入力周波数を変えなくても2倍の周波数で表示されていることになるからである。 | 入力周波数 | 200k$\Omega$ (規定) | 400k$\Omega$ (変更) | |:---:|:---:|:---:| | 200Hz | 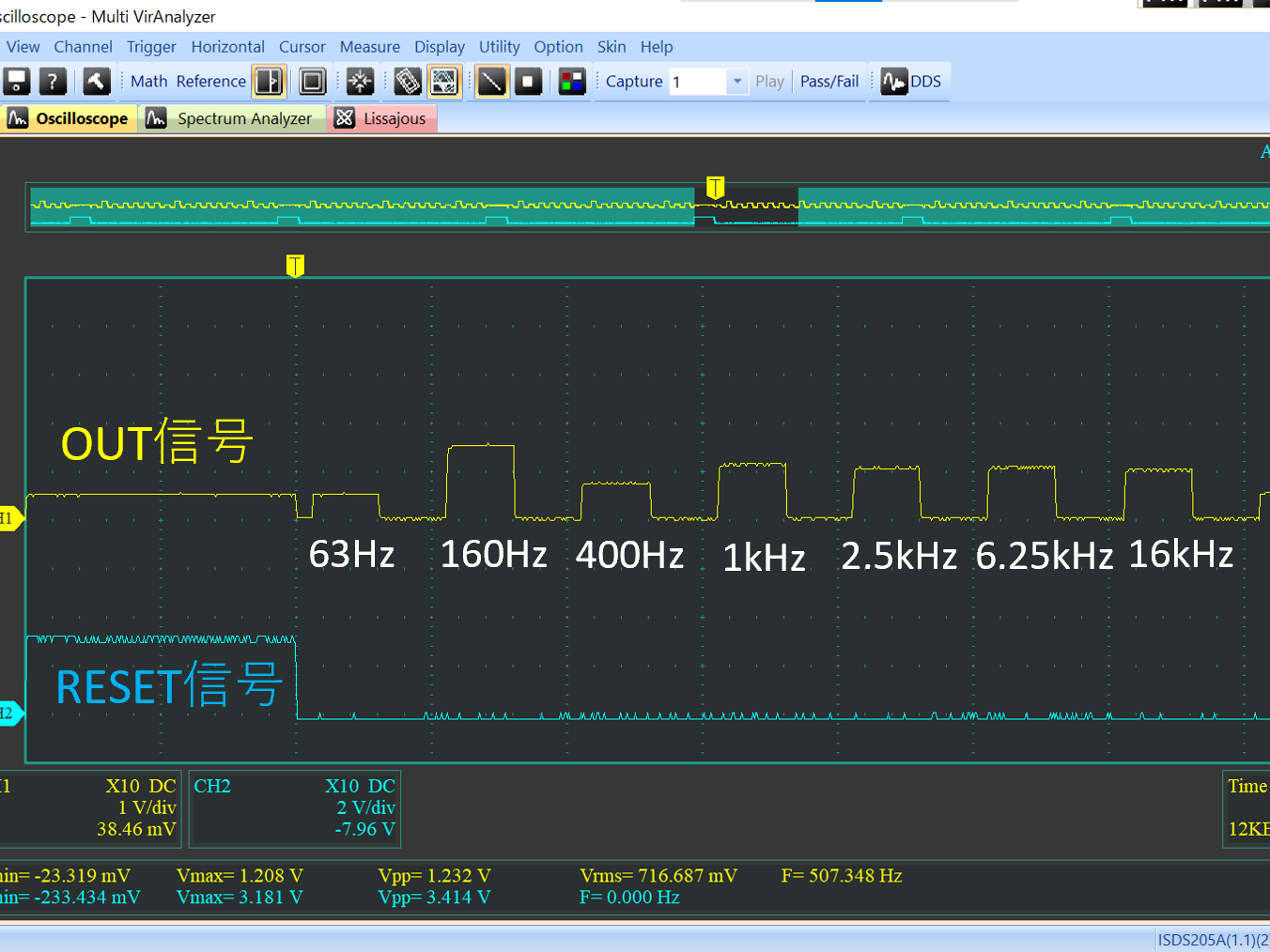 | 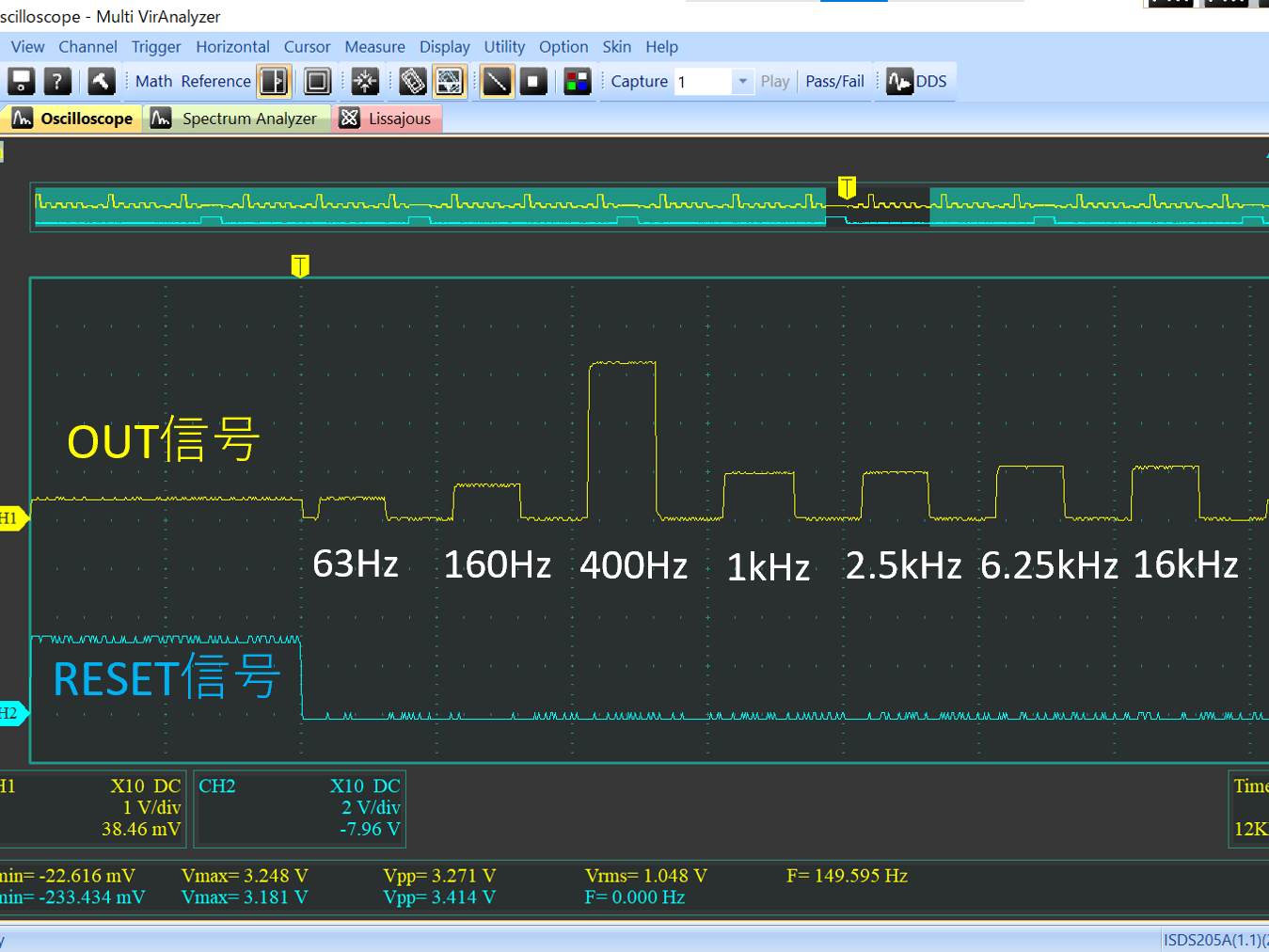 | | 500Hz | 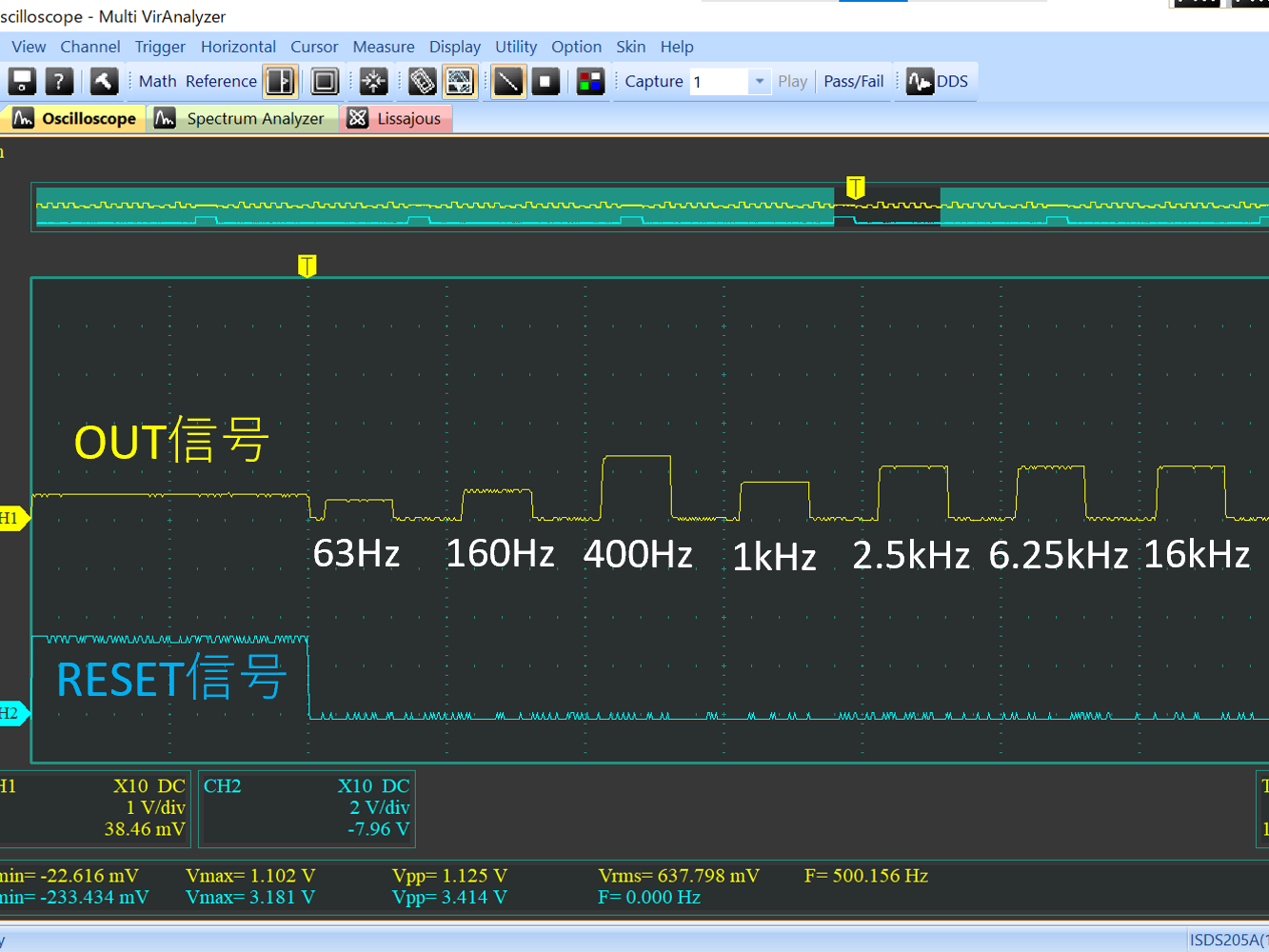 | 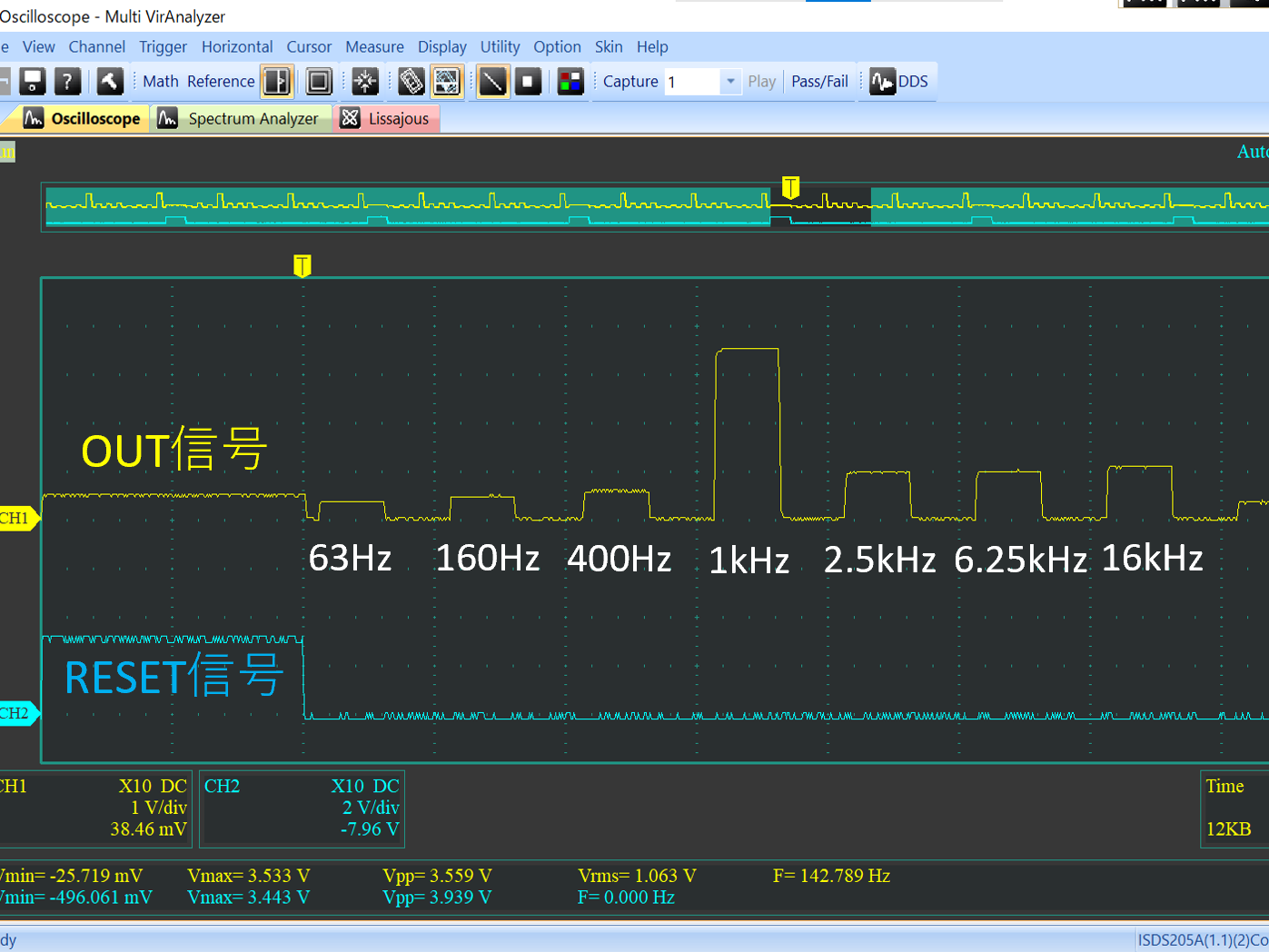 | 以上の場合から、**出力に表示されるピークの中心周波数は、CKINの抵抗値に比例して変動する**ことが確認できた。 # CKINに接続する素子と回路特性 前節でCKINに接続する抵抗に比例して出力に表示されるピーク周波数が変わり、それに応じてスペクトルの形状が変わることを確認した。この変化は偶然の産物なのだろうか？前節の結果が偶然ではなく、回路動作上妥当な特性変化であることが確認できるのであれば、MSGEQ7は推奨回路から外付け部品を変更することで、特性を自由に変えて動作させることができる。 本節では、CKINでのRC発振の発振周波数に着目して確認し、素子定数を変えることによる回路動作変化を考察していきたい。 ## CKINの発振 CKINに接続された抵抗とコンデンサは、内部回路の動作用のRC発振の周波数を決定する。例えば、推奨回路における定数(R=200k$\Omega$, C=33pF)においては、約100kHzのノコギリ波状に発振している。(下図) 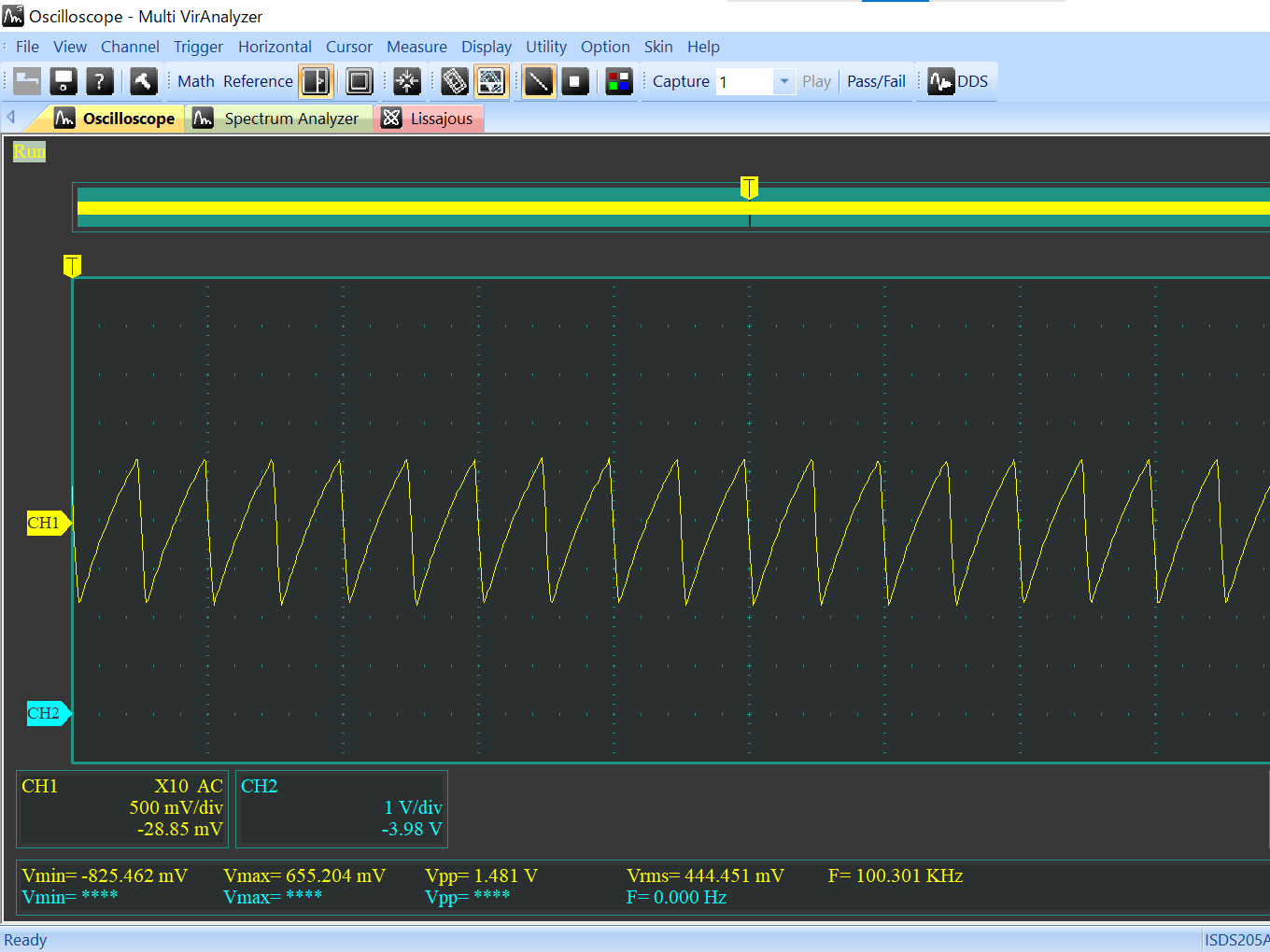 この発振周波数は、CKINに接続されている抵抗とコンデンサの容量(配線やプローブの寄生容量も含む)によって計算される時定数に応じて決定されると考えらえる。先述のピークの中心周波数の変化はCKINに接続した抵抗が大きくなると、IC内部での見かけの周波数が変化したことから、この発振周波数によって、出力するスペクトルのピーク中心周波数を決定していると考えられる。 以下では、CKINに接続する抵抗とコンデンサの値を変更してCKINの発振周波数を調べ、この仮説が正しいかどうかを検証する。  注：データシートによれば、CKINの発振周波数はC=33pF, R=200kOhmのとき、145kHz~180kHzであると記載されており、上図の発振周波数はデータシートに記載されている値よりも少し低く出ている。これは、測定回路をブレッドボードに組んでいることにより数pFの寄生容量が乗ったことに加え、CKIN端子に直接プローブを当てたことにより、プローブの入力容量も加わったことで、発振周波数が下がっていることが原因であると考えられる。以下測定結果も同じ回路を用いて行ったため、測定値には同様の影響を受けていると考えらえる。 ### 発振周波数の抵抗依存性 CKINに接続する容量を、10pF, 33pF, 68pF, 3300pFのそれぞれに固定し、CKINに接続する抵抗を変化させたときの発振周波数の変化を下図に示す。 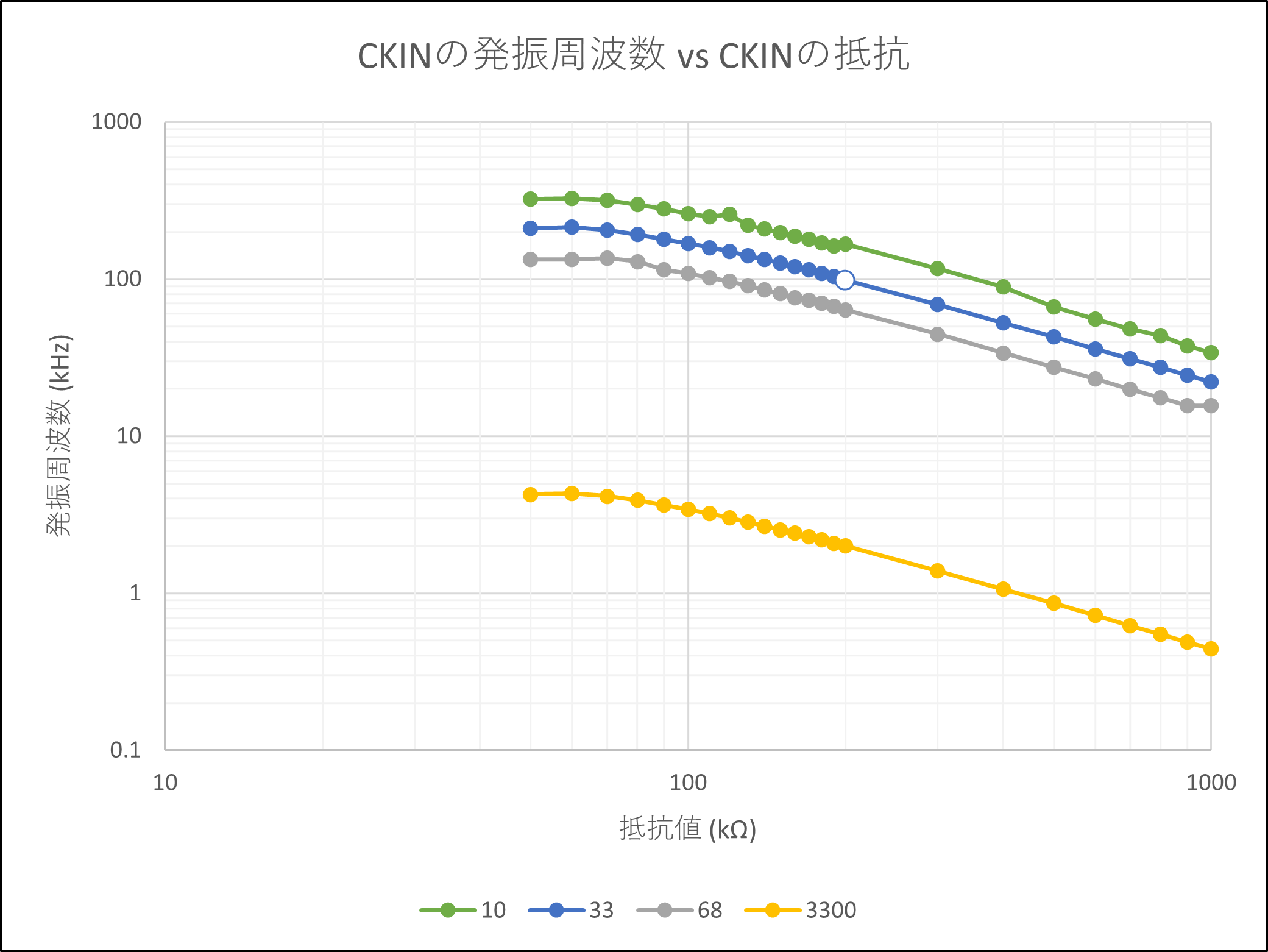 (色分けはCKINの容量　緑：10pF, 青：33pF, 灰：68pF, 黄：3300pF) 図から、接続する抵抗が100k$\Omega$から1M$\Omega$までの場合において、発振周波数が抵抗値に反比例することがわかる。前節で示した抵抗値の変更 (200k$\Omega$→500k$\Omega$、および、200k$\Omega$→400k$\Omega$)は、この反比例の関係にある範囲での変更であるため、この変更によるピークの中心周波数の変化と抵抗値の関係は、回路動作上関連のあるものであるといえる。 さらに図を見ると、この反比例の関係は、接続する容量に関わらず、抵抗値が100k$Omega$よりも低くなるとこの反比例の関係通りの発振周波数は得られず、50k$\Omega$未満では発振できなくなる。このため定数変更によりピークの中心周波数を変化させる場合、接続する抵抗は100k$Omega$以上が必要であると考えられる。 ### 発振周波数の容量依存性 CKINに接続する抵抗を、100k$\Omega$, 200k$\Omega$, 300k$\Omega$, 500k$\Omega$, 800k$\Omega$, 1000k$\Omega$ (=1M$\Omega$,)にそれぞれ固定し、接続するコンデンサと発振周波数の関係をプロットすると以下のようになる。 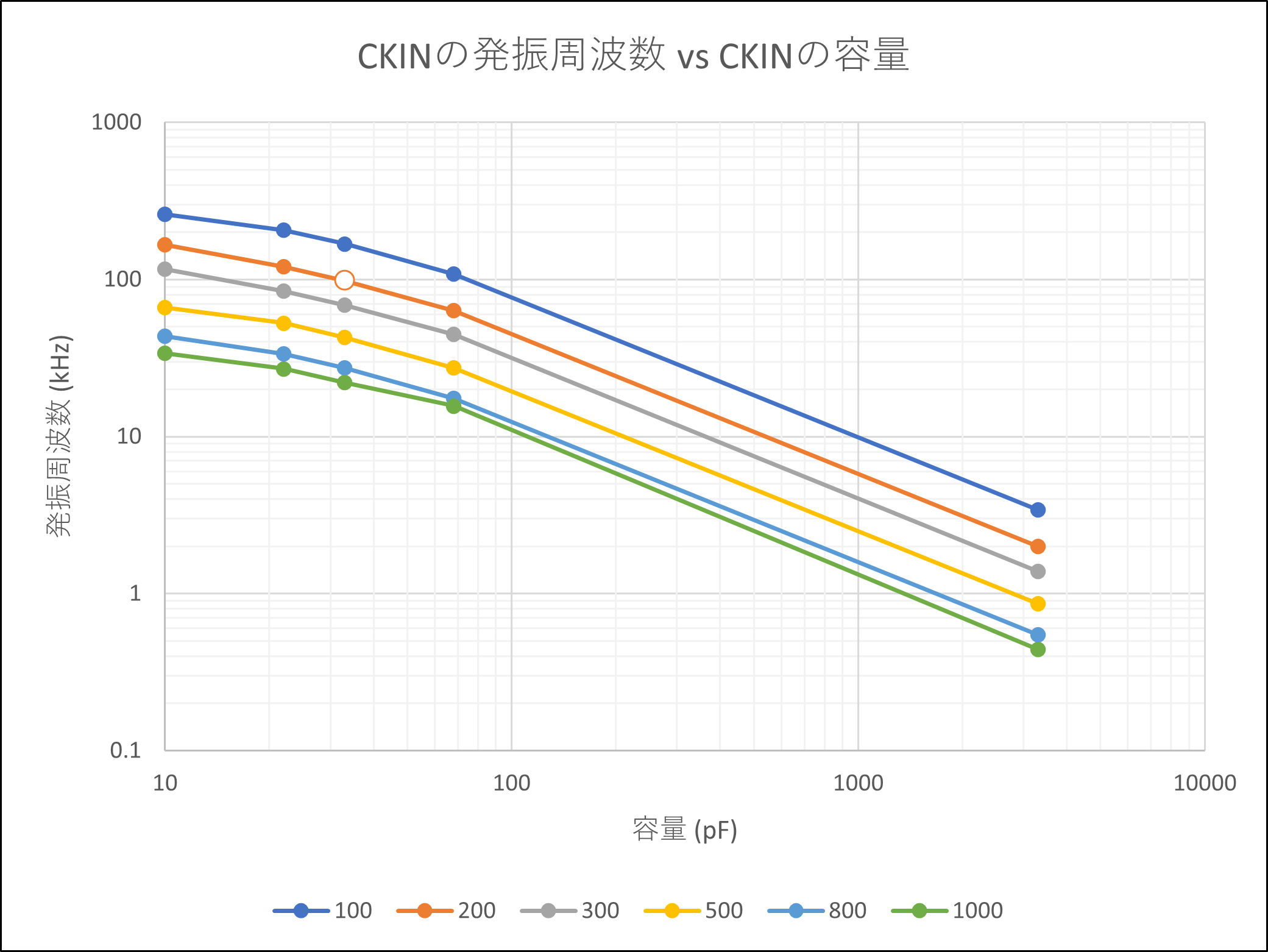 (色分けはCKINの抵抗　青：100k$\Omega$, 橙：200k$\Omega$, 灰：300k$\Omega$, 黄：500k$\Omega$, 水色：800k$\Omega$, 緑：1000k$\Omega$) 上図から、容量を大きくすることにより発振周波数が低下するが、抵抗の時と異なり、単純な比例または反比例の関係にはないことが読み取れる。これは、回路上の寄生容量の影響を強く受けるため容量依存性の測定は難しいことや、内部回路の動作が容量値により大きく変化することが原因であると考えらえる。 # ピークの中心周波数との相関関係 以上の測定から、CKINに接続する抵抗と回路動作の特性に以下の関係があることを確認した。 1. 出力端子に出力されるスペクトルのピーク中心周波数は、CKINに接続する抵抗に比例して大きくなる。 これは、IC内部における見かけの周波数がCKINに接続する抵抗に反比例して小さくなるためである。 1. CKINの発振周波数は、CKINに接続する抵抗の抵抗値に反比例する。(100k$Omega$~1M$Omega$の場合のみ) この関係により、CKINに接続する抵抗値と出力のピーク中心周波数の関係は、回路動作の観点から考察しても比例することと考えらえる。 ### 各ピークの中心周波数の算出式 データシートに記載されている7つのピークを、周波数が低いほうから$P_{00}, P_{10}, \cdots, P_{60}$と名付け、そのピークの中心周波数を$F_{Pn0} (n=0,1,\cdots,6)$と名付ける。以上の測定と考察により、データシートの推奨回路から、CKINに接続する抵抗$R$のみを変更した場合、各ピークの周波数$F_{Pn}(R)$は、推奨回路におけるピーク周波数$F_{Pn0}$ に対して以下のように変化する。 $$ F_{Pn}(R) = F_{Pn0} \times \frac{R}{200k\Omega} $$ また、データシートより、 $$F_{Pn0} = 63 \mathrm{Hz}, 160 \mathrm{Hz}, 400 \mathrm{Hz}, 1 \mathrm{kHz}, 2.5 \mathrm{kHz}, 6.25 \mathrm{kHz}, 16 \mathrm{kHz}$$ であることから、ピーク間の中心周波数の関係はおおよそ、 $$ F_{Pn0} = 1\mathrm{kHz} \times 2.5^{n-3} \enspace\enspace (n=0,1,\cdots,6) $$ と表すことができるので、抵抗値$R$に対する各ピークの中心周波数は以下のように表される。 $$ F_{Pn}(R) = 1\mathrm{kHz} \times 2.5^{n-3} \times \frac{R}{200k\Omega} \enspace\enspace (n=0,1,\cdots,6)$$ # まとめ 本記事では、MSGEQ7というICの動作を外付け部品に着目して測定し、出力波形の変化と回路動作の変化が一致したことから、外付け部品の変更により、データシートに記載されている以上の応用ができることを示唆した。 最後に、本記事で達成できた点と、今後の課題をまとめる。 ==達成できた点 ・MSGEQ7の推奨回路の動作を確認し、データシートに記載されている動作ができることを確認した。 ・推奨回路からCKINに接続する抵抗の抵抗値に比例して、出力されるスペクトルの中心周波数が高周波側にシフトすることを確認した。 ・上記シフトがCKINでのRC発振の発振周波数の変化と相関があり、この周波数を変えることで各ピークの中心周波数を変えることができることを示した。== ++今後の課題 ・CKINの発振周波数の容量依存性について、フィッティングがうまくできず容量を変えたときの特性把握ができなかった。 ・CKINの発振周波数を変えることにより変更できるバンドパスフィルタの回路構成の調査++