コメント無し

# はじめに 2023年のMaker Faire Tokyo 2023やNT東京にIsolation Cubeというガジェットを展示しました． @[youtube](https://www.youtube.com/watch?v=w3pRgsE_wJo) Isolation Cubeは，1面8x8=64 LEDの正方形マトリクスを6枚用いて正６面体（ 合計384LED）のCubeディスプレイに９軸のIMUセンサを用いてセンサの角度に合わせてディスプレイ表示を更新することで，いつも同じ向きに画像を呈示することができるデバイスです． 今回はより球体に近づけるべく新規に基板を起こして一枚50LEDの正五角形基板から成る正１２面体（600LED）に拡張してみました． 今まではマイコンにESP32を使用していましたが，LED数が増えてきたのでマルチコアで画面を分割して高速化を図るアイデアです． ESP32だと２コアなので１コア300LEDとなりますが，SPRESENSEは６コアあるので，メインUIコア＋４コア（１コアで150LEDを担当）する実装を目指します． ### モチベーション 球体ディスプレイを作るモチベーションについては以前にオープンエッジデバイス研究会で話しているので、そちらを。。

### 完成イメージ # 部品 ## SPRESENSE 今回はSpresenseさんから以下の製品をお借りして実装しました． ### メインボード  [製品情報](https://elchika.com/promotion/spresense2023/#:~:text=Spresense%20%E3%83%A1%E3%82%A4%E3%83%B3%E3%83%9C%E3%83%BC%E3%83%89-,%E8%A3%BD%E5%93%81%E6%83%85%E5%A0%B1,-%E6%8B%A1%E5%BC%B5%E3%83%87%E3%83%90%E3%82%A4%E3%82%B9) ここは説明不要だと思います． コアが６つもあるので，600個のLEDを分散して制御することができれば速度的にも有利です．IMUの回転角度情報から全てのLEDの仮想座標の３次元回転を個別に計算しなければならないのでかなりの計算量となるため，分散処理は必須と言っても良いものです． また，メインボードにLiPo用のDCDCを備えるため，DCDC用の基板を用意する必要がなく，LEDへの電力共有もEXT_VDD経由で大きい電流も出力できそうです． ### LTE拡張デバイス 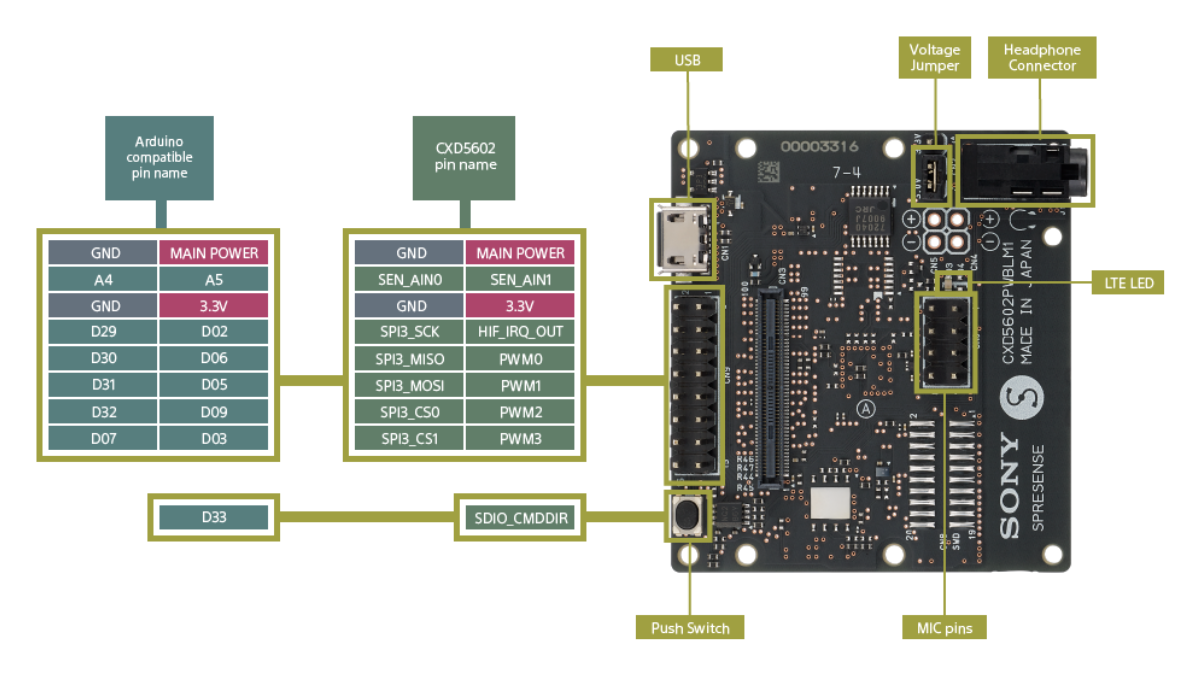 サンプル提供いただいたものは拡張ボードだったのですが，Isolation Sphereに格納するには大きすぎたので，手持ちのLTE拡張ボードを使用しました． Isolation sphereの正１２面体部分の内部にちょうど収まるサイズなので，そのまま収納します． 要求する機能としては表示する画像を格納するためのSDカードが欲しかったのと，UIやデータ転送のためにSIMが使えるならワンチャン．．．．と思ったためです．欲しかった機能はSDカードのみなので，SPI接続で．．．とも思ったのですが，ボール内に収まりそうなのでそのまま行きます． ### SPRESENSE用Qwiic接続基板  [製品情報](https://www.switch-science.com/products/6318) これと[BMI270](https://nextstep.official.ec/items/66165488)の両方をサンプル提供いただいたのですが，どちらが使えるかわからず，現時点ではIsolation Cubeで使い慣れているBNO055が接続可能なQwiic接続基板を採用しています．Qwiicだとケーブルが邪魔になるので，どこかの機会でBMI270も試してみたいと思います． ### BLE1507(BLE serialization firmware)  [製品情報](https://elchika.com/promotion/spresense2023/#:~:text=BLE%20serialization%20firmware)-,%E8%A3%BD%E5%93%81%E6%83%85%E5%A0%B1,-BLE1507(NUS%20firmware) こちらもサンプル提供いただきました． もともとESP32を採用していた理由がBLEもしくはWiFiが使える（ボールとして完全に閉じた形状＆全面ディスプレイになるため，電源ONなどUI操作をボタンとして配置できないため無線機能が必須）こと，だったのでこのデバイスを見つけた時に「おお，これならSPRESENSE使えるやん，しかもマルチコア数多い！」となって採用を決定したのでした． ## 表示用LED ### WS2812C-2020  [秋月電子でも販売している](https://akizukidenshi.com/catalog/g/gI-15068/)Neopixelベースのマイコン内蔵RGB LEDです．2020の名の通り2mm角という非常に小さなLEDです． WS2812-2020のシリーズには二種類（他方はWS2812B-2020）あり，その差は消費電力です．WS2812C-2020は5mAとWS2812B-2020の12mAと比較して小さい電流量なので，大量のLEDをLiPoなどの限られた電源で駆動させるのに向いています（当然暗くなりますが．．） このLEDを50個直列で配置するための正五角形基板を起こしました．  中心から螺旋状にシリアル配線してあります．所々にある穴は熱対策＆ネジ穴として外骨格を固定することを想定していましたが，現時点ではただの穴です．  裏側には配線およびコンデンサが配置されています．

接続して表示してみるとこんな感じ． ## IMU ### BNO055  現状で個人的には一番信頼できるIMUです．BNO085という後継もあるのですが一部使いにくいところがありこちらを愛用しています． ３次元回転にQuaternionを使っておりリソースが有限な中で直接Qaternionが関数から取得できるのは助かります． BNO055はキャリブレーションが不要かつドリフトもかなり抑えられており，Isolation Sphereのような完全封じ込め型のデバイスには助かります． ## 電源  3.7v 2000mahの充電式リチウムポリマー電池, 104040 LiPo電池になります。 40mmx40mmのサイズで、正１２面体に内接する最大立方体の１辺が約40mmなのでこのサイズをチョイス。メインボードに接続して使用します。 # 設計 ## 正１２面体 ### 基本設計思想 Isolation Sphereを作成するにあたって、重要な正12面体の諸元とそれらを作成するための基本設計を行います。 実はMaker Faire Tokyo 2023においてすでに一度正12面体のバージョンを作成していました。  このときには次のような内骨格構造をしていました（若干５角形のサイズも小さかったのですが。。）構造的には内部のマイコンやバッテリーが安定していたのですが、内部の容量が小さくなり（さらに配線の余裕を考えていなかったので）配線がギッチギチになってしまい「組み立てるとどこかが断線する」状態になっておりあえなくお蔵入りとなってしまいました。 そこで今回は最終目標である球体に近づけるため、球体の外殻（内側が正１２面体）を作成し、その外殻パネルにLED基板を貼り付ける外骨格構造を採用しました。 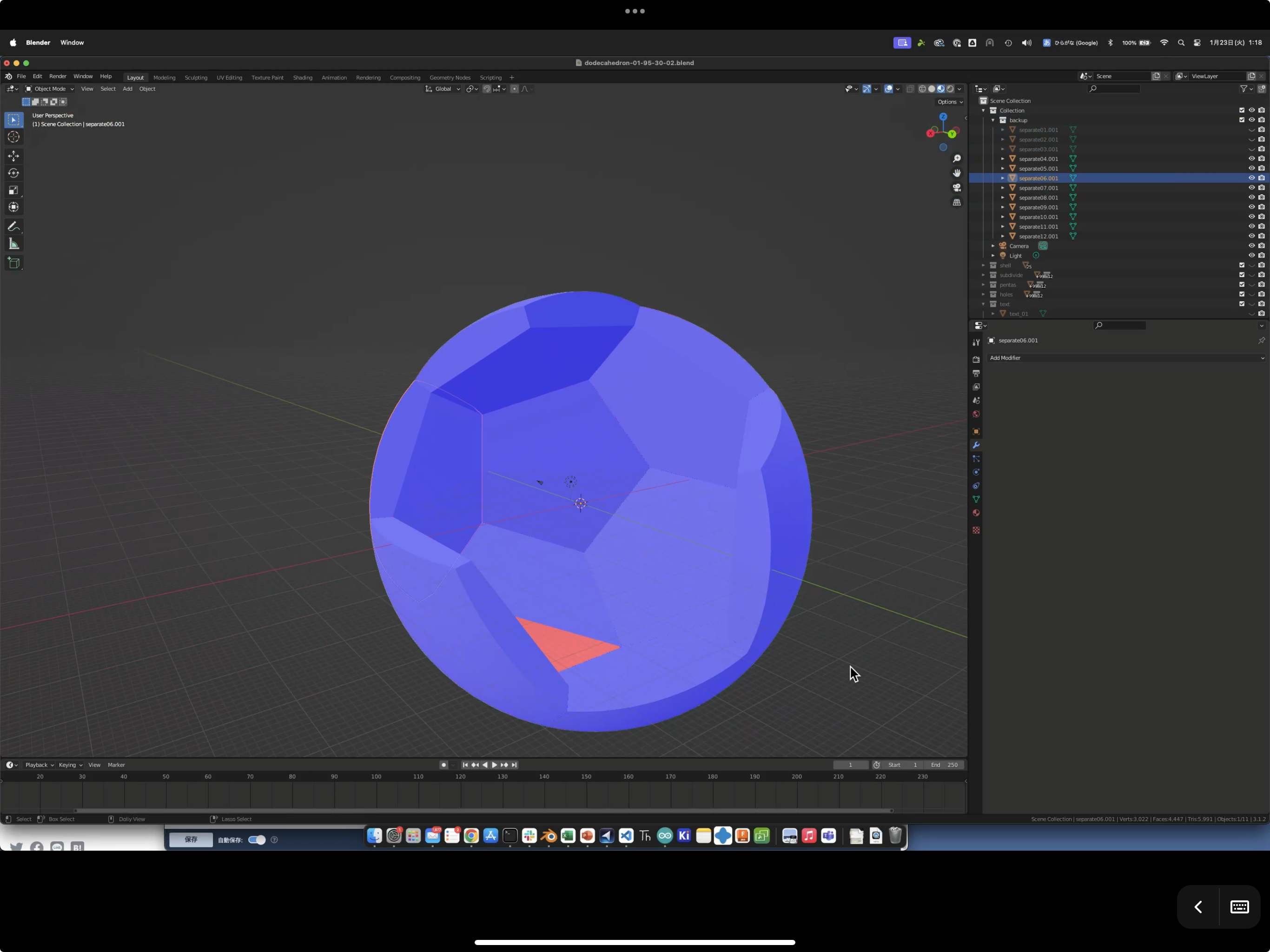 外骨格には内側の基板に配置されたLEDから外側の球まで穴を開け、球表面をボロノイ分割で600分割することで全面をディスプレイにすることができています。 これが外骨格の１基板分。

（黒レジンで作成したら光の拡散量が少なくなってしまったので、後に白レジンに変更） これをパネルとして組み合わせて球体にします。そうすると内部に骨格を配置する必要がないので内部の容積が十分確保できるようになり、SpresenseもLTE拡張ボードまで収納することができるようになりました。 ３Dプリンタで出力するときには３パネルを１セット（150LED）として４セット用意してこれを組み合わせて球体を形成します。SPRESENSEの場合はこの１セットを１コアが担当することを想定しています。

基板は平面・外殻は球体となっているので基板の周辺は球表面までの距離が近く歪が増え、基板重心付近では遠くなるため、若干視野角が異なることがどの程度画像に影響するか、はひとつ大きな課題になります。 ## 600LEDの配置 さて、球表面をｎ個に均等分割する方法というのはかなり難しく、理論的な方法はなかなか見つかりません。 今回設計した外殻球はφ100mm、内部の正１２面体の外接球がφ80mmとなっています。この外殻球表面に600LED（600LED÷12面体＝50LED/基板）を均等に配置する、という問題を考えます。 ### 一般化螺旋集合 解析的に解く方法はないだろうか？といろいろと探してみたのですが、私の要求に合うものがなかなか見つかりません。 一つ「[一般化螺旋集合](https://blog.panicblanket.com/archives/3778)」というものがあるのですが、この方法で600LEDを配置してみるとこのようになります。 @[youtube](https://youtu.be/0GsdxohajtE?si=YKieayR3R3wrCN-E) わかるでしょうか？この方法だと一様分布ではありますが螺旋方向の「スジ」ができてしまうのです。 Isolation Sphereのコンセプトは「回転させても絵が変わらない」というものです。しかしこのLEDの配置パターンだと上下に「極」ができてしまい、これを回転させるとどうしてもパターンが回転していることがわかってしまう。 球を回転させてもどこが「極」かわからない、となる必要があるのです。 ### Icosphere IcosphereというのはBlenderなどのCGソフトで球を表現するための方法の一つです。 球の表現の代表的な方法は、上のIcosphereとUV sphereというものです。 UV Sphereというのは、 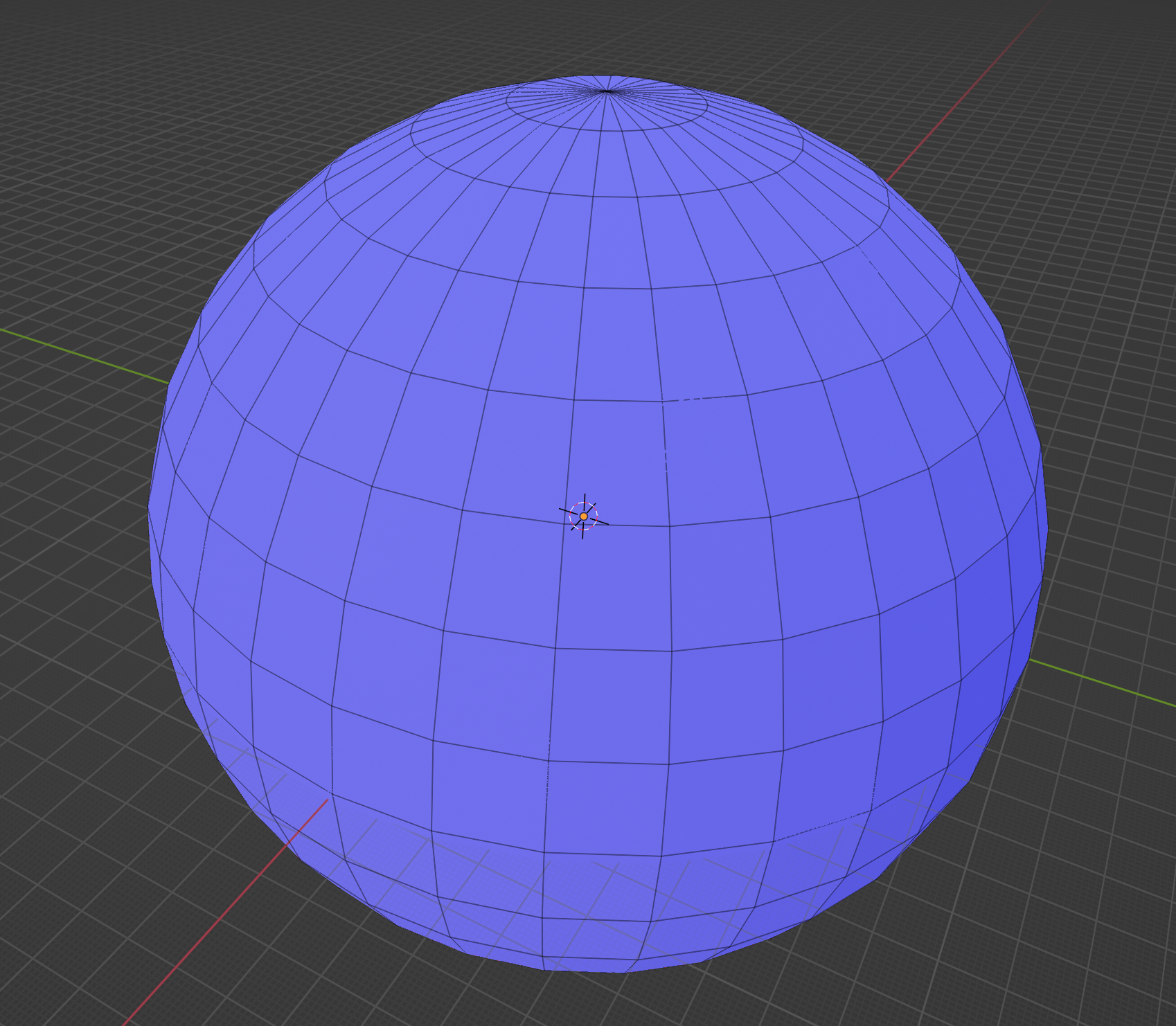 このように、緯度と経度で構成される球です。そのためテクスチャマッピングの貼り付けなどには非常にやりやすいメリットがありますが、北極・南極に点が集中するため、その部分が歪みやすいデメリットがあります。 対して、Icosphereというのは、  正多面体をsubdivide分割して細かくしていく球の表現方法です。正多面体の性質として極性を持たないため、回転してもどこが極かはわからないのです。 理想的ではあるのですが、図に示すように複雑性の上がり方が極端で自分で個数を制御できないのです（左からsubdivide=2→3→4）。 任意の数（Isolation Sphereの場合は600）の配置を行うことができないため、今回も採用は見送りました。 ### 逐次的な方法 最終的に採用した方法がこちら @[youtube](https://youtu.be/Au8QosJG8wA?si=FrItu_LpA4WdDRp-) UNITYを用いて、内部球（動画中の青い球）に重力を設定し、大気圏のようなもの（動画中の半透明の白い球）を設定し、このこの球の内側に衝突判定を設定することでボールがはみ出すことを防ぎます。 そこに任意数（ここでは600）のボール（動画中の緑球）を配置してお互いが衝突しながら最適配置を探す。。。という方法です。 詳細は以前に書いた[ブログ](https://tajmahal0707.hatenablog.com/entry/2023/06/08/074602)があるのでそちらを・・・ ## LED球体の設計 これまででLED 600個を球体表面に配置することができました。これを基板上では50x12の配置に、球表面では均等部分布にする必要があります。また、外殻球表面の穴を円筒にしてしまうと円筒間に隙間ができてしまい球表面全体をディスプレイにする際に問題になります。 そこで、基板と接する部分は円筒で、球表面上ではボロノイ分割にすることにします。こんな感じ。  ### voronoi分割 うまくいったら絶対エモいので、頑張りましたｗ @[blog](https://styly.cc/ja/tips/blender-geometrynodes-nyu/) @[blog](https://styly.cc/ja/tips/blender/nimi-blender-voronoi/) いろいろvoronoiを作る方法は紹介されています。しかし球表面に対して適用しているものがなかなか見つからず、苦労しました。 Isolation Sphereでは使用しませんでしたがこんなサイトもあります。 @[blog](https://www.voronator.com/) @[github](https://github.com/tylerjereddy/py_sphere_Voronoi) このようなライブラリも存在するのですが、自分の望んだ動作にならないため、オリジナルで作ることにしました。 #### Delaunay多角形 上で配置した600点の3次元位置はすでに計算できています。しかしこの点群から辺・面を繋いでポリゴンを生成するのはちょっと面倒です。 この点群は定義から全て球表面上にあり、均等に近ければ近いほど各点を繋いだポリゴンは正三角形に近くなることがわかります。正三角形に近くなればなるほどこのDelaunay多角形から作るvoronoi多角形は6角形になります。 また、同時にすべての点が球表面上にあるためこの点の集合は凸多面体であることもわかります。 そこでpythonで凸包を生成するプログラムを作成しました。 ライブラリにはopen3dを使います。 ソースコードの一部。（このままコピペでは動きませんがエッセンスはこんな感じ） ``` python:点群→凸包の生成 import open3d as o3d import pandas as pd import plotly as py import plotly.express as px import numpy as np from stl import mesh points = [] for i, d in df.iterrows(): p = d[['x', 'y', 'z']].values points.append(list(p)) pointcloud = o3d.geometry.PointCloud() # pointcloud.points = o3d.utility.Vector3dVector(df[['x', 'y', 'z']].values) pointcloud.points = o3d.utility.Vector3dVector(points) hull, _ = pointcloud.compute_convex_hull() hull_ls = o3d.geometry.LineSet.create_from_triangle_mesh(hull) hull_ls.paint_uniform_color((0, 1, 0)) hull.compute_vertex_normals() o3d.io.write_triangle_mesh(stl_filename, hull) o3d.visualization.draw_plotly([pointcloud, hull_ls]) ``` 出力結果はこんな感じ。 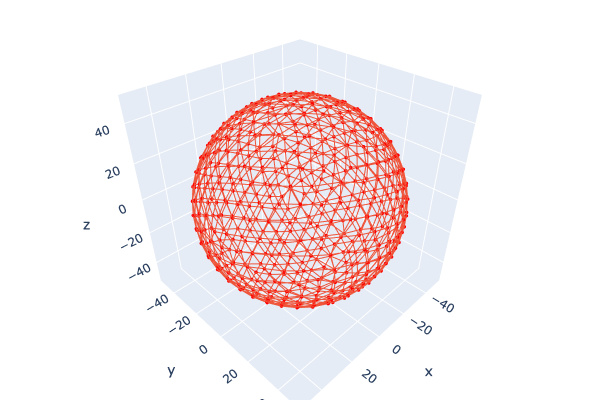 これをstl形式でファイル出力します。  stlファイルで出力することで、各3角形の3次元位置を個別に取得することができるため、後のvoronoi計算処理が楽になります。 ### voronoi多角形の作成 Delaunay多面体ができたのであれば、そこからvoronoi多角形に拡張します。 @[wikipedia](https://ja.wikipedia.org/wiki/%E3%83%9C%E3%83%AD%E3%83%8E%E3%82%A4%E5%9B%B3) Delaunay多角形をstlで出力したのは、stlの出力フォーマットが３角形を形成する頂点座標を３角形ごとに出力されるためです。 ```python:stl読み込み from stl import mesh stl_data = mesh.Mesh.from_file(filename ) print(stl_data.points) ``` これを実行すると > [[-49.31912 7.78104 2.6608098 ... -49.956623 1.3397751 -1.5939546] [-48.49622 6.584802 10.235096 ... -44.360455 9.363192 21.082712 ] [ 47.784668 -9.589299 -11.165614 ... 45.983433 -17.109419 -9.632838 ] ... [ 47.255344 -12.76661 10.195397 ... 45.92527 -19.05439 5.272538 ] [ 45.92527 -19.05439 5.272538 ... 42.422623 -25.259659 7.891177 ] [ 44.41393 -19.146568 12.681166 ... 42.422623 -25.259659 7.891177 ]] となり、stl.pointsは配列として9x「面の数」となっており、この9はDelaunay三角形の３頂点の3次元座標を表しています。 voronoiの定義から各Delaunay三角形の座標＆辺情報が必要で、voronoiはdelaunay三角形の頂点を母点とし、母点でつくる辺の垂直二等分線によって分割される面をvoronoi多角形として、voronoi面を形成する頂点をvoronoi頂点と定義されます。

このように黄線で定義されるDelaunay三角形に対して水色線のvoronoi多角形を定義する。 ここでvoronoi頂点も外殻球表面上の点となるため、頂点で構成される点群も凸包であることがわかります。 そこで先程の凸包プログラムを適用することでvoronoi多角形の形状も取得することができます。 その結果がこちら 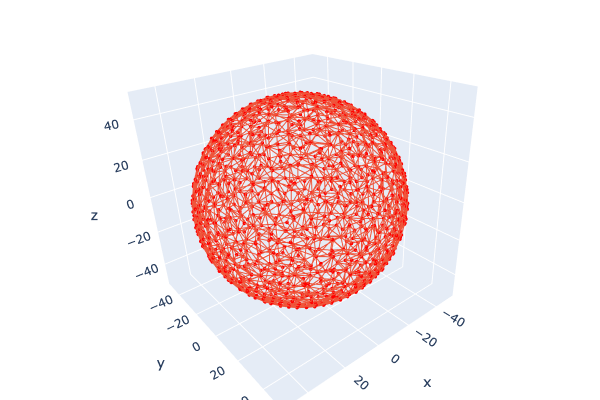  ### LEDからの円筒穴の作成 基板上のLEDの位置と、対応する外殻球上の点を結んだパイプ形状（以後ミミズ）を作成する。 こんな感じ。

この大量のミミズを外角球からboolean演算でくり抜くことでLEDからの導光路を確保する。 ```python:blender_booleans import bpy boolean_type = 'DIFFERENCE' root_object = bpy.data.objects['shell-05'] selected_objects = bpy.context.selected_objects for obj in selected_objects: print('boolean', obj.name) name = 'bool-' + obj.name.split('-')[1] + '-' + obj.name.split('-')[2] bool01 = root_object.modifiers.new(type="BOOLEAN", name=name) bool01.object = obj bool01.operation = boolean_type bpy.context.view_layer.objects.active = obj bpy.ops.object.modifier_apply(modifier=name, report=True) ``` これはコード内でroot_object名を指定して、booleanしたいオブジェクトを選択した状態でこのpythonを実行すると、root_objectに対して選択したオブジェクトをすべてboolean演算するマクロです。 これを使い各パネルごとに各色のミミズをboolean演算する。 大量のmodifierが生成されてかなり重くなるが、これを一括で適用する裏技を紹介しておく。 modifierがあるオブジェクトを選択して、  meshを選択することで、このオブジェクトに付いているmodifierが一括適用される。 覚えておくと良い。 ### voronoi 穴の作成 voronoi多角形の頂点（多くは６点、たまに５点や７点）とLEDの中心（正１２面体の五角形上の点）をまとめて点群にすると、この点群は凸包となる。 この凸包をポリゴン化するとvoronoi多角形を底面とする多角錐（voronoi錐）ができます。 作成したvoronoi錐がこんな感じ。 | 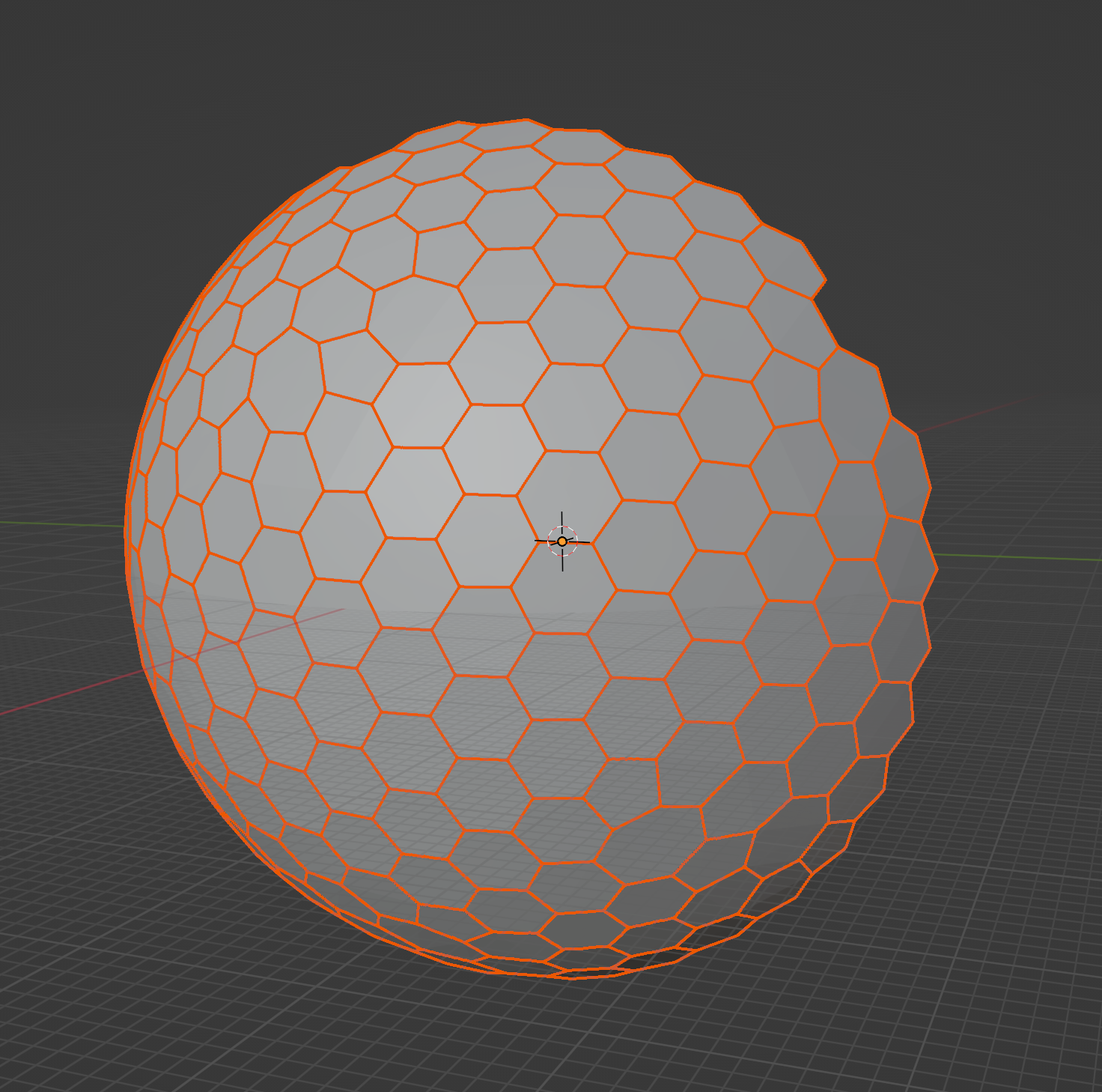 | | |:---:|:---| これを外殻からbooleanで削除することで外殻にvoronoiの穴があきます。 ただ、その前にvoronoi錐にBevelを適用することでvoronoi錐の角が丸くなりより滑らかな穴が開けられます。 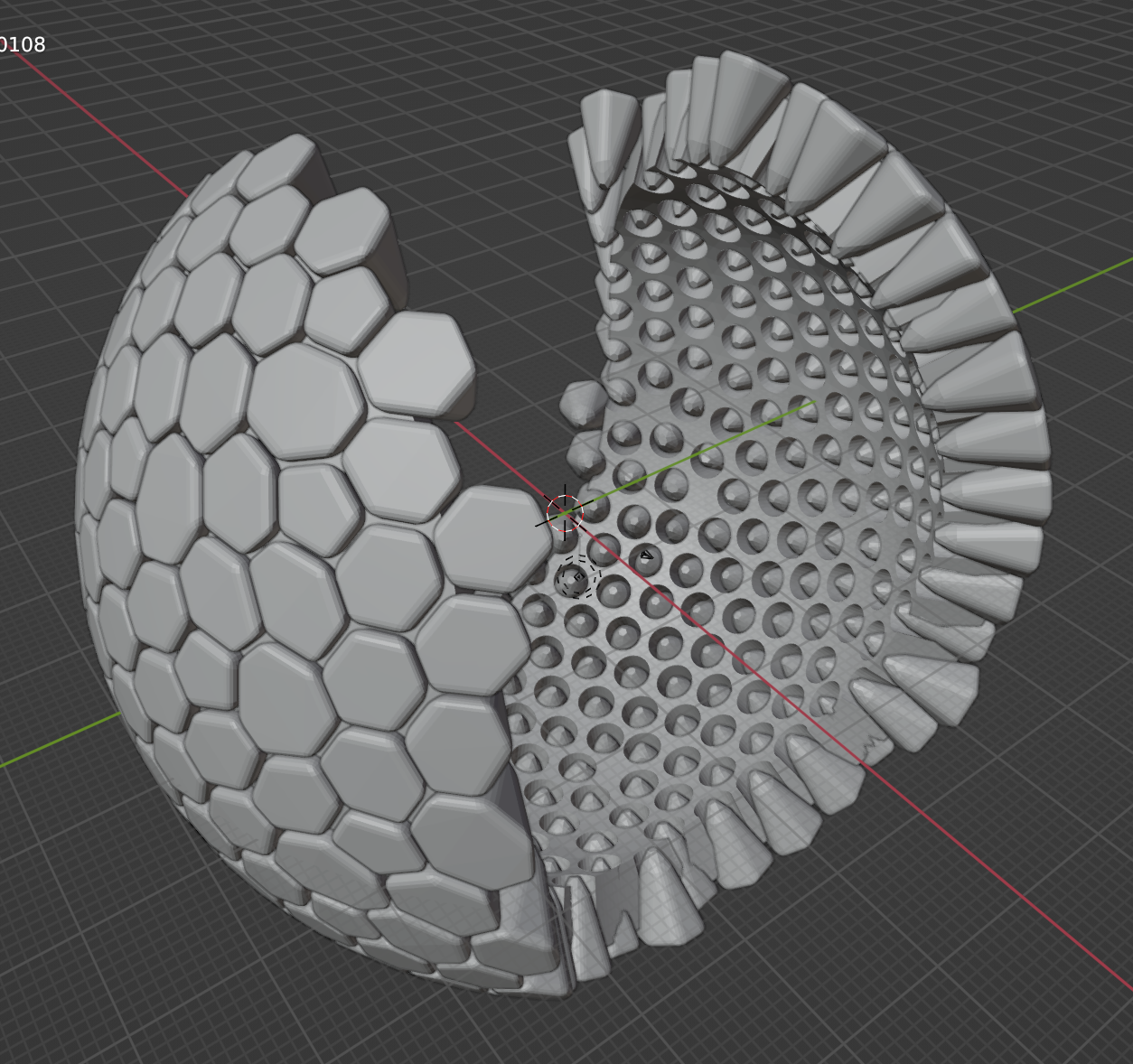 これで外殻球の完成。 @[youtube](https://youtu.be/4m_QSiS4KtM?si=UaREAnfV81zA0ORN) ### 葬送のフリーレン でこの球体配置が話題になっていたようです。 @[youtube](https://www.youtube.com/watch?v=odP8k8_zrlc) 私はここで見たのですが

その時にはフリーレンのことを知らずにマジレスしてしまいました。私の回答も一部を5角形（もしくは７角形）に置換することで球体表面の６角形分割を行うことができるようになる派でしたｗ ちょうどこのようなガジェットを作っていた最中だったので、タイムリーすぎて思わず反応してしまいました。 # 動作