オペアンプを用いたバンドパスフィルタの特性を計算で求める

先日 オペアンプを用いたバンドパスフィルタの動作を理解する という記事を書きました。そこで登場したバンドパスフィルタのゲイン、およびカットオフ周波数を計算で求めてみよう、というのが本記事の目的です。

次の回路のうち、U2A、R2、C2、R3、C3 が構成するバンドパスフィルタの動作を解析します。

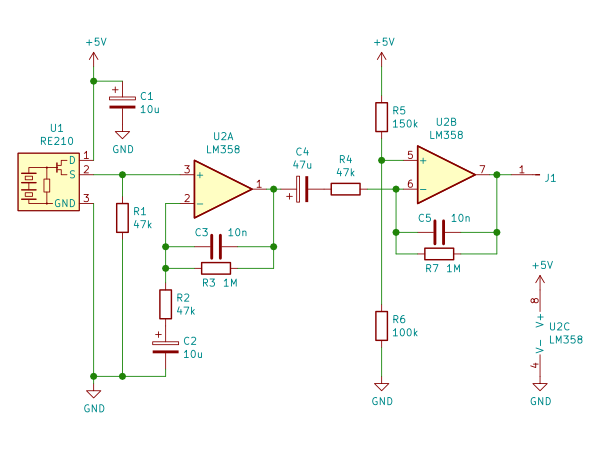
この回路の役割は、目的の微小な交流成分を増幅するのと同時に、ノイズや直流成分(*)をカットすることです。目的の交流成分とは人や動物が動くことによるセンサの変化です。すなわち、高々数 Hz の交流成分ということになります。人間や動物の動きは通常 10Hz とかにはなりませんからね。

*) 焦電センサの S 端子からは、数 V 程度の直流に微小な交流信号が重畳された信号が出力されます。

ゲインの計算

ここでは記号法による計算を行ってゲインを求めてみます。記号法とは複素数によりインピーダンスや電圧、電流を計算する方法です。記号法は多くの教科書に登場します。私が参考にしたのは 基本からわかる電気回路 の 12 章です。

R2、C2、R3、C3 のインピーダンスは次の通りです。

$\dot{Z_{R_2}}=R_2$

$\dot{Z_{C_2}}=-jX_{C_2}=-j\frac{1}{\omega C_2}$

$\dot{Z_{R_3}}=R_3$

$\dot{Z_{C_3}}=-jX_{C_3}=-j\frac{1}{\omega C_3}$

$\omega$ は角周波数といって、周波数 $f$（Hz）を用いると $\omega = 2\pi f$ と表せます。

R2、C2 は直列接続なので、合成インピーダンスを $\dot{Z_2}$ とすると

$\dot{Z_2}=\dot{Z_{R_2}}+\dot{Z_{C_2}}=R_2-jX_{C_2}$

R3、C3 は並列接続なので、合成インピーダンスを $\dot{Z_3}$ とすると

$\frac{1}{\dot{Z_3}}=\frac{1}{\dot{Z_{R_3}}}+\frac{1}{\dot{Z_{C_3}}}=\frac{1}{R_3}+\frac{1}{-jX_{C_3}}$

すなわち

$\dot{Z_3}=\frac{R_3X_{C_3}}{jR_3+X_{C_3}}=\frac{R_3}{j\frac{R_3}{X_{C_3}}+1}$

U2A の + 端子に入力される信号を $\dot{v}$ とします。$\dot{v}$ は焦電センサの出力なので、数 V 程度の直流信号に、振幅が数 mV ～数 10mV 程度の交流信号が重畳されたものだと考えられます。

オペアンプは通常動作時はイマジナリショートの状態ですので、- 端子の電圧も $\dot{v}$ となります。R2 に流れる電流を $\dot{I}$ と置くと

$\dot{v}=\dot{Z_2}\dot{I}$

の関係が成り立ちます。また、U2A の出力端子の電圧 $\dot{V}$ は次式となります。

$\dot{V}=\dot{v}+\dot{Z_3}\dot{I}$

U2A によるバンドパスフィルタのゲインを $G(\omega)$ とすると

$G(\omega)=\left|\frac{\dot{V}}{\dot{v}}\right|=\left|1+\frac{\dot{Z_3}\dot{I}}{\dot{v}}\right|=\left|1+\frac{\dot{Z_3}}{\dot{Z_2}}\right|$

となります。C2、C3 を無視すると $G(\omega)=1+\frac{R_3}{R_2}$ となり、抵抗の比で増幅率が設定される増幅器であることが分かります。

ゲインの実際の値

実際の部品定数を当てはめて計算すると、ゲインは次のようになります。

さらに細かく数値計算してみると 2.32Hz 付近で最大となり、そのときのゲインは 21.83 倍となりました。

低域側のカットオフ周波数

バンドパスフィルタの低域側のカットオフ周波数を求めてみます。カットオフ周波数は、ゲインが最大値の -3dB になった点での周波数とされています。$-3=20\log{x}$ を解くと $x=10^{-\frac{3}{20}}\approx 0.7079$ となります。（$x$ はゲイン）

$10^{-\frac{3}{20}}$ は扱いに困るよく分からない数値ですが、実は $\frac{1}{\sqrt{2}}\approx 0.7071$ で近似できます。というより本来は逆で、$\frac{1}{\sqrt{2}}$ を使うべきところを $10^{-\frac{3}{20}}$ で近似しているのですが。本来はカットオフ点のゲインは $20\log{\frac{1}{\sqrt{2}}}$dB となるのですが、近似値を用いて簡単に「カットオフ点は -3dB」と言っているわけですね。

ということで、ゲインの最大値を $G_M$、低域側のカットオフ周波数を $\omega_L$ とすると

$G(\omega_L)=\frac{1}{\sqrt{2}}G_M$

が成り立ちます。先ほど求めたゲインに $\omega_L$ を代入すると

$G(\omega_L)=\left|1+\frac{\dot{Z_3}(\omega_L)}{\dot{Z_2}(\omega_L)}\right|$

ですが、計算をしやすくするために近似を行います。

• 低域側のカットオフ点付近では周波数が低いため、C3 は高い抵抗値となる（$X_{C_3}\to\infty$）と考え、$\dot{Z_3}\approx R_3$ と近似します。
• $\left|\frac{\dot{Z_3}}{\dot{Z_2}}\right|\gg 1$ なので、$\left|1+\frac{\dot{Z_3}}{\dot{Z_2}}\right|\approx\left|\frac{\dot{Z_3}}{\dot{Z_2}}\right|$ と近似します。

するとゲインは次のように計算できます。

$G(\omega_L)\approx\left|\frac{\dot{Z_3}(\omega_L)}{\dot{Z_2}(\omega_L)}\right|\approx\left|\frac{R_3}{R_2-jX_{C_2}(\omega_L)}\right|$

右辺を計算すると次のようになります。

$\left|\frac{R_3}{R_2-jX_{C_2}}\right|=\left|\frac{R_3(R_2+jX_{C_2})}{R_2^2+X_{C_2}^2}\right|=\frac{\sqrt{(R_2R_3)^2+(R_3X_{C_2})^2}}{R_2^2+X_{C_2}^2}=\frac{R_3}{\sqrt{R_2^2+X_{C_2}^2}}$

したがって

$\frac{R_3}{\sqrt{R_2^2+X_{C_2}^2}}=\frac{1}{\sqrt{2}}G_M$

ここで $G_M$ を求めてみます。$G_M$ は $G(\omega)$ が最大になる点なので

$G(\omega)=\left|1+\frac{\dot{Z_3}}{\dot{Z_2}}\right|=\left|1+\frac{\frac{R_3}{j\frac{R_3}{X_{C_3}}+1}}{R_2-jX_{C_2}}\right|$

が最大となるときを考えると $X_{C_2}\to 0$、$X_{C_3}\to\infty$ のときです（正確には $X_{C_2}\to 0$ と $X_{C_3}\to\infty$ が同時に成り立つことはありませんが、ここでは簡単のために、C2、C3 を除去したときがフィルタの理論的な最大ゲインだと考えることにしました）。このとき

$G_M=1+\frac{R_3}{R_2}\approx\frac{R_3}{R_2}$

となります。よって

$\frac{R_3}{\sqrt{R_2^2+X_{C_2}^2}}=\frac{1}{\sqrt{2}}\frac{R_3}{R_2}$

計算すると

$\sqrt{2}R_2=\sqrt{R_2^2+X_{C_2}^2}$

$2R_2^2=R_2^2+X_{C_2}^2$

$R_2^2=X_{C_2}^2$

したがって

$X_{C_2}=R_2$

$X_{C_2}=\frac{1}{\omega_L C_2}$、$\omega_L=2\pi f_L$（$f_L$ はカットオフ周波数）を代入して計算すると

$f_L=\frac{1}{2\pi R_2C_2}\approx 0.34\, \mathrm{Hz}$

高域側のカットオフ周波数

バンドパスフィルタの高域側のカットオフ周波数を求めてみます。低域側と考え方は同じですが、用いる近似を変えます。

• 高域側のカットオフ点付近では周波数が高いため、C2 は低い抵抗値となる（$X_{C_2}\to 0$）と考え、$\dot{Z_2}\approx R_2$ と近似します。
• $\left|\frac{\dot{Z_3}}{\dot{Z_2}}\right|\gg 1$ なので、$\left|1+\frac{\dot{Z_3}}{\dot{Z_2}}\right|\approx\left|\frac{\dot{Z_3}}{\dot{Z_2}}\right|$ と近似します。

ゲインは次のように計算できます。

$G(\omega_H)\approx\left|\frac{\dot{Z_3}(\omega_H)}{\dot{Z_2}(\omega_H)}\right|\approx\left|\frac{\frac{R_3X_{C_3}(\omega_H)}{jR_3+X_{C_3}(\omega_H)}}{R_2}\right|$

右辺を計算すると

$\left|\frac{\frac{R_3X_{C_3}}{jR_3+X_{C_3}}}{R_2}\right|=\left|\frac{R_3X_{C_3}}{R_2(jR_3+X_{C_3})}\right|=\left|\frac{R_3X_{C_3}(X_{C_3}-jR_3)}{R_2(R_3^2+X_{C_3}^2)}\right|$

$=\frac{R_3X_{C_3}}{R_2(R_3^2+X_{C_3}^2)}\sqrt{R_3^2+X_{C_3}^2}=\frac{R_3X_{C_3}}{R_2\sqrt{R_3^2+X_{C_3}^2}}$

したがって

$\frac{R_3X_{C_3}}{R_2\sqrt{R_3^2+X_{C_3}^2}}=\frac{1}{\sqrt{2}}G_M$

さきほどと同様に

$G_M\approx\frac{R_3}{R_2}$

とすると

$\frac{R_3X_{C_3}}{R_2\sqrt{R_3^2+X_{C_3}^2}}=\frac{1}{\sqrt{2}}\frac{R_3}{R_2}$

計算すると

$X_{C_3}=R_3$

$X_{C_3}=\frac{1}{\omega_H C_3}$、$\omega_H=2\pi f_H$（$f_H$ はカットオフ周波数）を代入して計算すると

$f_H=\frac{1}{2\pi R_3C_3}\approx 15.92\, \mathrm{Hz}$

近似の妥当性

カットオフ周波数を計算する過程で次のような近似を行いました。

1. $\left|1+\frac{\dot{Z_3}}{\dot{Z_2}}\right|\approx\left|\frac{\dot{Z_3}}{\dot{Z_2}}\right|$
2. 低域側のカットオフ点付近で $\dot{Z_3}\approx R_3$ （$X_{C_3}\to\infty$）
3. 高域側のカットオフ点付近で $\dot{Z_2}\approx R_2$ （$X_{C_2}\to 0$）

この近似が妥当なのかを考えてみます。もちろん立場によって判断の基準は変わると思いますが、今回は「焦電センサの出力を適切に取り扱う」場合に許容できる近似かどうか、という判断です。

近似 1 について。このバンドパスフィルタの通過域でのゲインは 21 倍程度ありますから、この近似は妥当と思います。

近似 2 について。$f_L$ 付近で C3 によるインピーダンスが無限大と思えるほど大きいかどうかがポイントです。そのために C3 のインピーダンスを計算したグラフを見てみます。

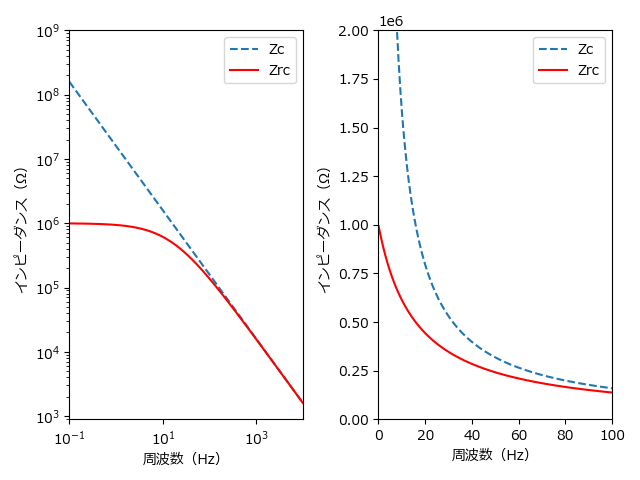
グラフの Zc は C3 によるインピーダンスを、Zrc は R3 と C3 による合成インピーダンスを表します。カットオフ周波数 0.34Hz 付近では Zc が十分に大きく（対数グラフの方で見ると 40MΩ 程度）、R3 が支配的であることが分かります。したがって近似 2 は妥当でしょう。

近似 3 について。$f_H$ 付近で C2 によるインピーダンスが無視できるほど小さいかどうかがポイントです。そのために C2 のインピーダンスを計算したグラフを見てみます。

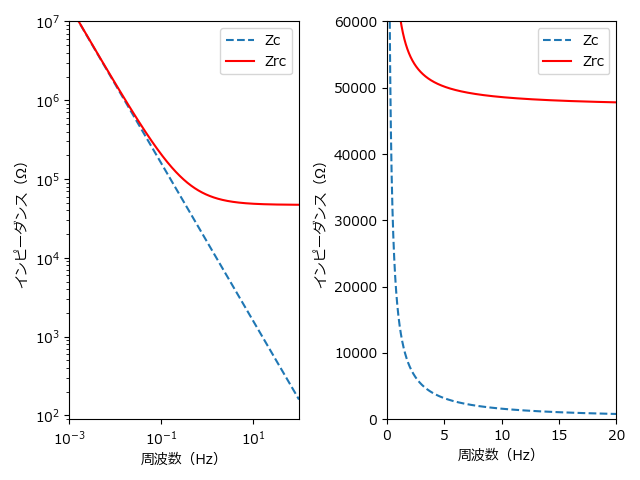
カットオフ周波数 15.92Hz 付近では C2 によるインピーダンスは 1kΩ 程度で、R2 = 47kΩ に比べて十分に小さいです。近似 3 も妥当でしょう。

まとめ

焦電センサ用のバンドパスフィルタのゲインは次式で表せます。

$G(\omega)=\left|1+\frac{\dot{Z_3}}{\dot{Z_2}}\right|$

カットオフ周波数は、低域側、高域側それぞれ次式で表せます。

$f_L=\frac{1}{2\pi R_2C_2}$

$f_H=\frac{1}{2\pi R_3C_3}$