角度計算には弧度法を用いています。もし電卓が度数法の場合は弧度法に変更するか、πを180に置き換えるなどして下さい。
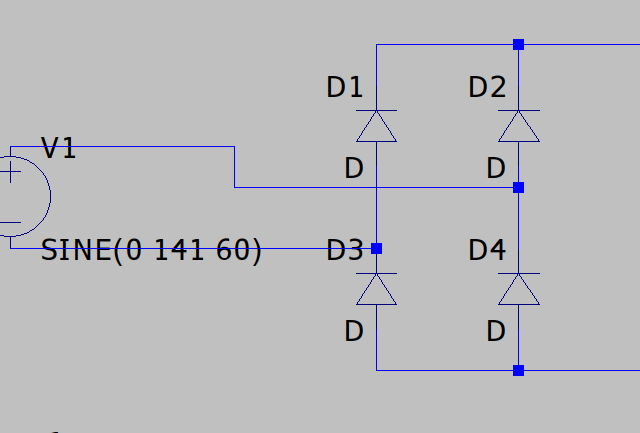
C=−2πfRo×ln(VoutmaxVoutmin)2π+sin−1(VoutmaxVoutmin)
ただし
VoutmaxVoutmin=η
とすると
C=−2πfRo×ln(η)2π+sin−1(η)
半波整流回路は、全波整流より波の間隔がさらにπ空くので
C=−2πfRo×ln(η)π+2π+sin−1(η)=−2πfRo×ln(η)23π+sin−1(η)
合ってるかは分からないけど...
まずRC並列回路の放電時の電圧は、初期の最大電圧をVmとして
VC=Vme−RCt
よりtは
t=−RC×ln(VmVC)
ただし、全波整流回路の放電が開始される際の角度はπ/2なので
t−2ωπ=−RC×ln(VmVC) ⋅⋅⋅A
また、正弦波交流の電圧瞬時式は
V=Vm×sin(ωt)
コンデンサが再充電される際は、角度がπ以上であるため
VC=Vm×sin(ωt−π)
より再充電が開始される時間tは
t=ω1(sin−1(VmVC)+π)⋅⋅⋅B
B式をA式へ代入し
2π+sin−1(VmVC)=−ωRC×ln(VmVC)
Cの式へ整理しVC=Voutmin,Vm=Voutmaxに変換してやると
C=−2πfRo×ln(VoutmaxVoutmin)2π+sin−1(VoutmaxVoutmin)
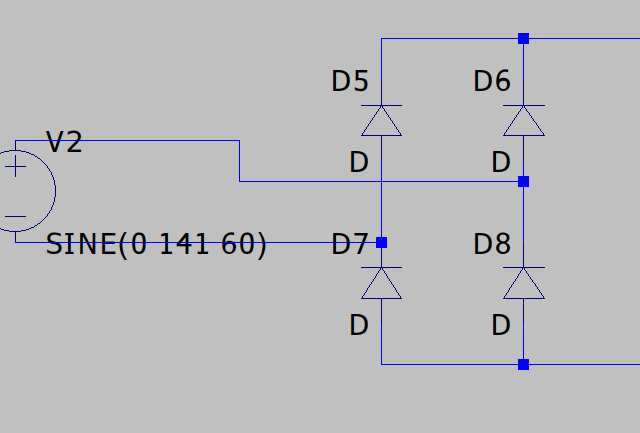
C=2πf(Voutmax−Voutmin)2π+sin−1(VoutmaxVoutmin)Iout
VC=C1∫idt
よりiはコンデンサ自身から発生しているので負になります。つまり
VC=−Cit+K
放電開始時t=π/(2ω)とおき、そのときVCはVmなので
K=Vm+2ωCπi
より
VC=Vm−Ci(t−2ωπ)
より
t−2ωπ=iC(Vm−VC)
この式に前述のB式を代入し
2π+sin−1(VmVC)=iωC(Vm−VC)
Cの式へ整理しVC=Voutmin,Vm=Voutmax,i=Ioutに変換してやると
C=2πf(Voutmax−Voutmin)2π+sin−1(VoutmaxVoutmin)Iout
半波整流回路の場合は
C=2πf(Voutmax−Voutmin)23π+sin−1(VoutmaxVoutmin)Iout
全波整流
C=−2πfRo×ln(VoutmaxVoutmin)2π+sin−1(VoutmaxVoutmin)
半波整流
C=−2πfRo×ln(VoutmaxVoutmin)23π+sin−1(VoutmaxVoutmin)
全波整流
C=2πf(Voutmax−Voutmin)2π+sin−1(VoutmaxVoutmin)Iout
半波整流
C=2πf(Voutmax−Voutmin)23π+sin−1(VoutmaxVoutmin)Iout




-
rily
さんが
2025/12/27
に
編集
をしました。
(メッセージ: 初版)
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/27
に
編集
をしました。
-
rily
さんが
2025/12/28
に
編集
をしました。
-
rily
さんが
2025/12/28
に
編集
をしました。
-
rily
さんが
2026/01/08
に
編集
をしました。
ログインしてコメントを投稿する