sanguisorba 2021年05月07日作成 (2022年01月22日更新) © MIT

セットアップや使用方法閲覧数

6273

sanguisorba 2021年05月07日作成 (2022年01月22日更新) © MIT

セットアップや使用方法閲覧数

6273

Wolfram Engine + Jupyter notebookで回路解析 (Windows)

Wolfram Mathematicaを個人で使うには高額すぎる。
そこで、無料で使えるWolfram EngineとJupyter notebookを使ってMathematica相当の環境を作ろうという話。

大学でWolfram Mathematicaのライセンスが無償配布されているという方はこの記事を見る必要ありません。

ちなみに、単純に回路解析をしたい場合はWolfram Alphaでも同じ事ができます。
https://www.wolframalpha.com/

後半の回路解析が間違っていたらコメントください

Q.どういうときにWolfram言語を使うの？
A.こういう回路を解析する時に使う。これを微積で計算するのは面倒くさい。

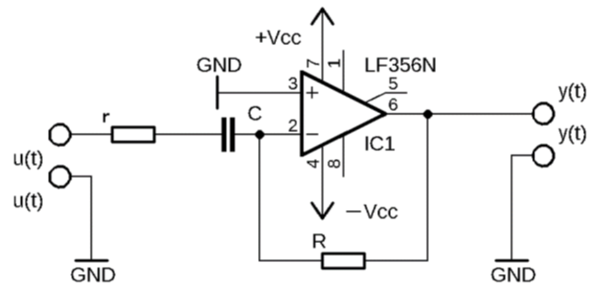
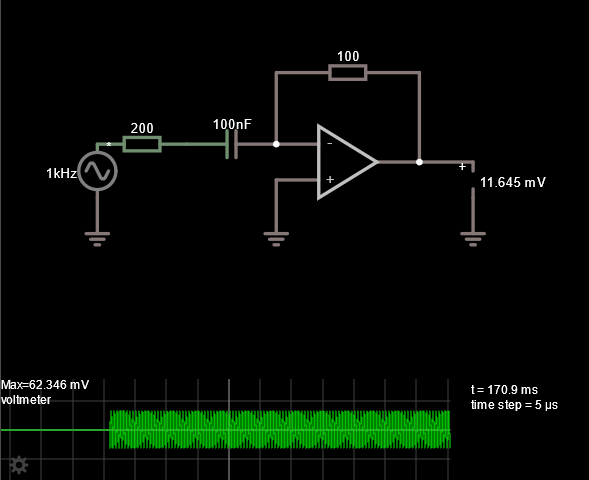
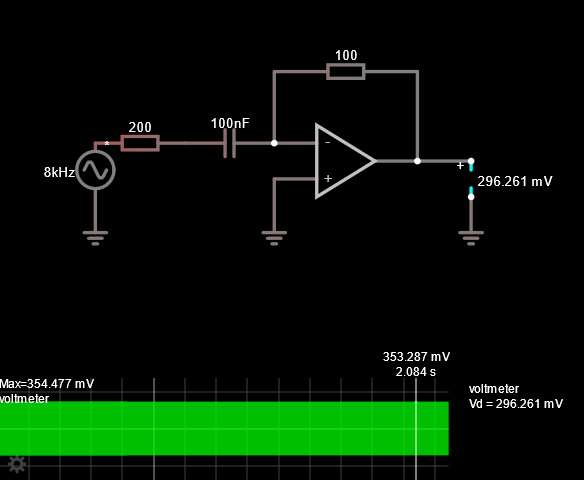
回路シミュレータによるとこのような出力電圧となるらしい。

大まかな流れ

ここから本体をダウンロード＆インストール
https://www.wolfram.com/engine/index.ja.php
Wolfram IDを作ってアクティベート（ダウンロード画面で次のステップとして書いてある事をするだけ）

これは大した作業じゃない。

Jupyter notebookを用いるにはPythonの導入が必要ですが、Pythonを使った事がない人には敷居が高いです。
そこで今回はAnaconda Individual パッケージを使用します。このPythonパッケージにはJupyter notebookが予め内蔵されています。

プラットフォームに合わせてダウンロードしてください
https://www.anaconda.com/products/individual
これをインストーラの指示に従って入れてください。
・All Users でインストール
・Add Anaconda 3 to the system PATH environment variable　のチェックは不要です。

このサイトから右上の緑色のCodeボタンを押してDownload Zipでダウンロードしてください。
https://github.com/WolframResearch/WolframLanguageForJupyter

解凍すると、WolframLanguageForJupyter-masterというフォルダの中にごちゃごちゃといろいろ入ってます。
このフォルダをそのままAnacondaのフォルダに移します。All Usersの場合、デフォルトのインストール先は
C:\ProgramData\Anaconda3
その後、Anaconda promptを起動して以下のコマンドを入力します

CD C:\ProgramData\Anaconda3\WolframLanguageForJupyter-master
.\configure-jupyter.wls add

その後、
jupyter kernelspec list
とコマンドを入力して、Available kernelsの中に"wolframlanguage"があれば成功です。
一回コマンドプロンプトを閉じて、改めてAnaconda 3 > Jupyter NotebookでJupyterを起動しましょう。

Jupyter NotebookはWebベースのアプリケーションなので起動するとコマンドプロンプトと同時にブラウザが起動して、そこにJupyterの画面が表示されます。

右上のNewタブにWolfram Languageがあればちゃんと追加できています。これを選択しましょう。

すると次のような画面が表示されます。

In [] : のテキストボックスにWolfram言語を入力します。
例えば5+2を計算したい場合、5+2と入力して上のRunを押す。
例えば不定積分を行いたい場合は Integrate[Cos[x],x]と入力してRunを押す。
※Wolram言語では三角関数の頭文字は大文字です。

そうすると次のように出力されます。

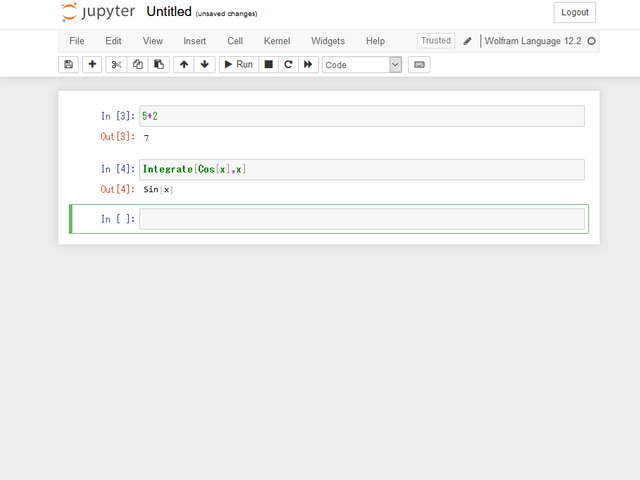
これがWolframです。

Wolfram言語については次のドキュメントを参照。
https://reference.wolfram.com/language/

今回は周波数特性をx軸に周波数、y軸に振幅比としてグラフに出力する事を目標とします。

Wolfram言語で回路解析をする場合はラプラス変換を用いて計算を行います。
そのため、回路方程式をラプラス変換によるs関数表記に変える必要があります。

回路を学習したことある人であれば、この３つの式は知っていると思います。

$V=RI$

$V=\frac{1}{C} \int I dt$

$V=L\frac{dI}{dt}$

s関数では、微分と積分を次のように表現します

$\frac{1}{s}= \int dt$

$s=\frac{d}{dt}$

従って、コイルとコンデンサの電圧と電流の関係式を次のように書き換えます。

$\mathcal{L}[V]=\frac{1}{sC}\mathcal{L}[I]$

$\mathcal{L}[V]=sL\mathcal{L}[I]$

これを基に回路方程式を立てます。

尚、ラプラス変換の記号は $\mathcal {L}$ 、逆ラプラス変換の記号は $\mathcal {L}^{-1}$ で表されます。

入力側の電流は

$\mathcal{L}[u(t)]=r\mathcal{L}[I]+\frac{1}{sC}\mathcal{L}[I]=\frac{sCr+1}{sC}\mathcal{L}[I]$

$\mathcal{L}[I]=\frac{sC}{sCr+1} \mathcal{L}[u(t)]$

出力側の電流は

$\mathcal{L}[y(t)]=R\mathcal{L}[I]$

$\mathcal{L}[I]=\frac{1}{R}\mathcal{L}[y(t)]$

入力電流と反転出力電流が等しいと仮定して

$\frac{sC}{sCr+1}\mathcal{L}[u(t)]+\frac{1}{R}\mathcal{L}[y(t)]=0$

$\mathcal{L}[y(t)]=-R\frac{sC}{sCr+1}\mathcal{L}[u(t)]$

一つ注意点として、入力電圧もラプラス変換をする必要があります。

ラプラス変換表から求めるのがセオリーですが、せっかくなのでWolframを用いて計算をしてみましょう。
LaplaceTransformの構文は


LaplaceTransform [**関数**, t, s]

です。中身の関数は時間tに関する表記となるように計算します。直流の場合は直流電圧をそのまま代入します。

以下は実行例です。( $cos(\omega t), 5, e^{-at}, 5cos(\omega t)$ )

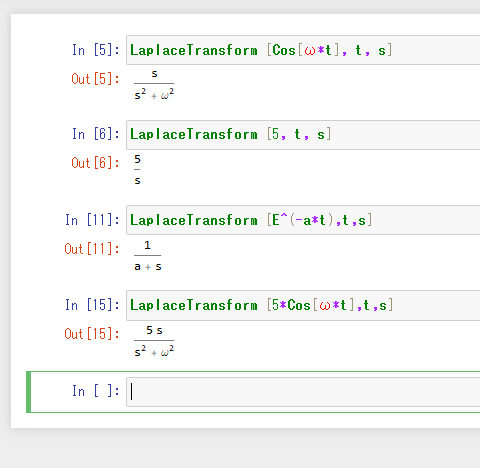
前書きで載せたシミュレーションの入力電圧は交流1Vなので $1\times cos(\omega t)$ のラプラス変換した値である

$\mathcal{L}[u(t)]=\frac{s}{s^2+\omega ^2}$

が入力電圧となります。ゆえに、

$\mathcal{L}[y(t)]=-R\frac{sC}{sCr+1}\mathcal{L}[u(t)]=-R\frac{sC}{sCr+1} \frac{s}{s^2+\omega ^2}$

となります。
先程、ラプラス変換を行ったので今度は逆ラプラス変換を行います。
さらに素子値を代入しても良いですが、この状態で逆ラプラス変換を行う事もできます。
InverseLaplaceTransformの構文は


InverseLaplaceTransform [**関数**, s, t]

です。sとtが逆になります。具体的にはこんな感じ。


In [16] : InverseLaplaceTransform [-R*(s*C/(1+s*C*r))*(s/(s^2+ω^2)),s,t]

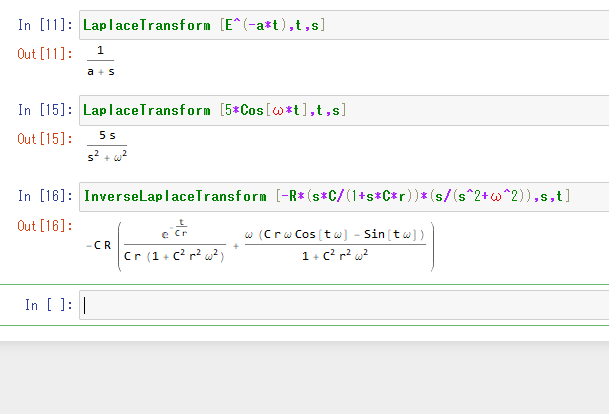
ちなみに、本家のWolfram Mathematicaで計算してもこんな感じ。

わかりやすく書くと、

$y(t)=\frac{CR\omega sin (\omega t) - C^2rR \omega ^2 cos (\omega t)}{C^2 r^2 \omega ^2 +1}-\frac{R}{r(C^2r^2 \omega ^2+1)} e^{- \frac{t}{Cr}}$

これが入力電圧cosωtに対しての出力電圧です。ただし定常状態ではexp項がほぼ0となるので

$y(t)=\frac{CR\omega sin (\omega t) - C^2rR \omega ^2 cos (\omega t)}{C^2 r^2 \omega ^2 +1}$

となります。

さっきの素子値を代入するとこんな感じになります。
$r=200\Omega$ , $R=100\Omega$ , $C=100\times10^{-9}F$


In [17] : InverseLaplaceTransform [-100*(s*10^(-7)/(1+s*10^(-7)*200))*(s/(s^2+ω^2)),s,t]

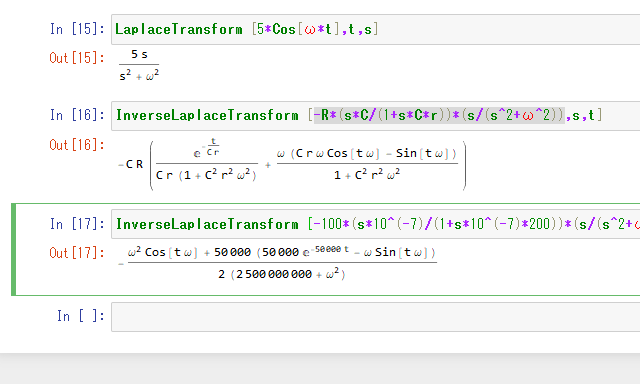
定常状態とすると、

$y(t)=\frac {50000\omega sin (\omega t)-\omega ^2 cos (\omega t)}{5 000 000 000 + 2 \omega ^2}$

ただし、

$\omega = 2 \pi f$

これで振幅を求めてみます。NMaxValueで求めました。

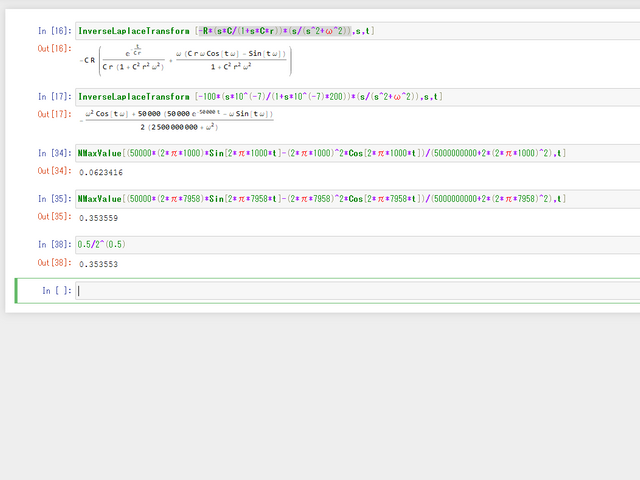
1000Hzの時62.34mV、7958Hzの時353.56mVとなりました。
回路シミュレータでの値と比べてどうでしょう？
概ね一致しているのではないでしょうか。

カットオフ周波数は

$f=\frac{1}{2 \pi fCr}$

です。シミュレーションで用いた素子値を代入すると7957.747となります。
この回路の最大振幅は $\frac{R}{r}=\frac{100}{200}=0.5$ です。
OPアンプでのカットオフ周波数は最大利得-3dBであり、振幅で表すと振幅Aに対して $\frac{A}{\sqrt{2}}$ です。
よさげな計算結果が得られましたが、どうでしょう。
また、高周波になるにつれて最大振幅比の0.5,つまり500mVに近づきます。


In [34] : NMaxValue[(50000*(2*π*1000)*Sin[2*π*1000*t]-(2*π*1000)^2*Cos[2*π*1000*t])/(5000000000+2*(2*π*1000)^2),t]
Out[34] : 0.0623416

In [35] : NMaxValue[(50000*(2*π*7958)*Sin[2*π*7958*t]-(2*π*7958)^2*Cos[2*π*7958*t])/(5000000000+2*(2*π*7958)^2),t]
Out[35] : 0.353559

In [39] : NMaxValue[(50000*(2*π*7957.747)*Sin[2*π*7957.747*t]-(2*π*7957.747)^2*Cos[2*π*7957.747*t])/(5000000000+2*(2*π*7957.747)^2),t]
Out[39] : 0.353553

In [38] : 0.5/2^(0.5)
Out[38] : 0.353553

In [41] : NMaxValue[(50000*(2*π*50000)*Sin[2*π*50000*t]-(2*π*50000)^2*Cos[2*π*50000*t])/(5000000000+2*(2*π*50000)^2),t]
Out[41] : 0.493785

In [42] : NMaxValue[(50000*(2*π*100000)*Sin[2*π*100000*t]-(2*π*100000)^2*Cos[2*π*100000*t])/(5000000000+2*(2*π*100000)^2),t]
Out[42] : 0.498424

In [43] : NMaxValue[(50000*(2*π*200000)*Sin[2*π*200000*t]-(2*π*200000)^2*Cos[2*π*200000*t])/(5000000000+2*(2*π*200000)^2),t]
Out[43] : 0.499605

周波数と振幅比（最大値）をプロットすると、次のようになります。今回はPlotを用います。

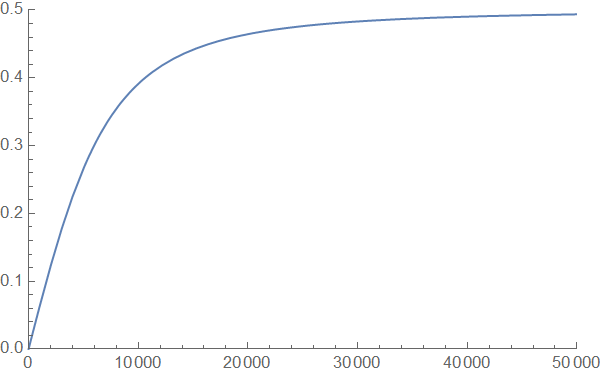
入力はω-> 2πx, t -> yとして


In [51] : Plot [NMaxValue[(50000*2*π*x*Sin[2*π*x*y]-(2*π*x)^2*Cos[2*π*x*y])/(5000000000+2*(2*π*x)^2),y],{x,1,50000}, PlotRange ->{{0,50000},{0,0.5}}]

Plot内部でPlotRangeを指定してやらないとy軸の表示域が変な事になります。

今回提示した回路はコンピュータを使わないと解けないほど複雑という訳ではないです。ただ計算が面倒なだけ。

まず前提として覚えておかなければならない式

$V=RI$

$V=\frac{1}{C} \int I dt$

$V=L\frac{dI}{dt}$

これだけを用いて回路方程式を立てます。

まず入力電圧を決める必要があります。シミュレーションと同じ１Vの正弦波 $cos (\omega t)$ とします。

入力側の電流は

$rI+\frac{1}{C}\int I dt=cos(\omega t)$

電荷に関する式に変換して微分方程式を解くと、（ここが面倒くさい）

$\frac{dQ}{dt}+\frac{Q}{Cr}=\frac{cos(\omega t)}{r}$

今回は未定係数法で求めます。
通常係数は $c_1, c_2 ...$ という感じに表しますが、コンデンサと被るので $b$ で表記すると

$Q=b_1e^{-\frac{t}{Cr}}+b_2 cos (\omega t)+b_3 sin (\omega t)$

$b_2$ , $b_3$ は特解を代入すればよい。

$\frac{d[b_2 cos (\omega t)+b_3 sin (\omega t)]}{dt}+\frac{b_2 cos (\omega t)+b_3 sin (\omega t)}{Cr}=\frac{cos(\omega t)}{r}$

$[-b_2 \omega sin (\omega t)+b_3 \omega cos (\omega t)]+\frac{b_2 cos (\omega t)+b_3 sin (\omega t)}{Cr}=\frac{cos(\omega t)}{r}$

ここからできる連立方程式

$-b_2 \omega+\frac{b_3}{Cr}=0$

$b_3 \omega+\frac{b_2}{Cr}=\frac{1}{r}$

これを解いて

$b_2=\frac{C}{\omega ^2 C^2 r^2+1}$

$b_3=\frac{\omega C^2r}{\omega ^2 C^2 r^2+1}$

だから、

$Q=b_1e^{-\frac{t}{Cr}}+\frac{C}{\omega ^2 C^2 r^2+1}cos (\omega t)+\frac{\omega C^2r}{\omega ^2 C^2 r^2+1}sin (\omega t)$

$b_1$ はt=0におけるコンデンサの電荷の初期値はQ=0だから

$0=b_1+\frac{C}{\omega ^2 C^2 r^2+1}$

$b_1=-\frac{C}{\omega ^2 C^2 r^2+1}$

よって

$Q=-\frac{C}{\omega ^2 C^2 r^2+1}e^{-\frac{t}{Cr}}+\frac{C}{\omega ^2 C^2 r^2+1}cos (\omega t)+\frac{\omega C^2r}{\omega ^2 C^2 r^2+1}sin (\omega t)$

あとは電荷を微分すれば電流になるので

$I=\frac{dQ}{dt}=\frac{\omega ^2 C^2 r cos (\omega t) - \omega C sin (\omega t)}{\omega^2 C^2 r^2 +1} + \frac{1}{\omega^2 C^2 r^2 +1} \frac{1}{r}e^{-\frac{t}{Cr}}$

出力側の電流は

$y(t)=RI$

$I=\frac{y(t)}{R}$

入力電流と反転出力電流が等しいと仮定して

$\frac{\omega ^2 C^2 r cos (\omega t) - \omega C sin (\omega t)}{\omega^2 C^2 r^2 +1} + \frac{1}{\omega^2 C^2 r^2 +1} \frac{1}{r}e^{-\frac{t}{Cr}}+\frac{y(t)}{R}=0$

$y(t)=\frac{-\omega ^2 C^2 r Rcos (\omega t) + \omega C Rsin (\omega t)}{\omega^2 C^2 r^2 +1} - \frac{1}{\omega^2 C^2 r^2 +1} \frac{R}{r}e^{-\frac{t}{Cr}}$